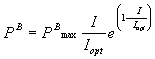Dynamic
behaviour of photosynthesis-irradiance curves determined from oxygen production
during VARIABLE incubation periods.
Macedo1 M. F.,
Ferreira2 J. G. & Duarte3 P.
1 Dept. of Environmental Sciences &
Engineering, Faculty of Sciences and Technology, New University of Lisbon, 2825
Monte de Caparica, Portugal. E-mail: mfmd@helios.si.fct.unl.pt
2 Dept. of Environmental Sciences &
Engineering, Faculty of Sciences and Technology, New University of Lisbon, 2825
Monte de Caparica, Portugal. http://tejo.dcea.fct.unl.pt
3 Dept. of Sciences & Technology, Fernando
Pessoa University, Praça 9 de Abril 349, 4200 Porto, Portugal. E-mail: nop57746@mail.telepac.pt
Abstract: The
production and consumption of oxygen were analysed in phytoplankton populations
using a fast biomass-concentration technique. The variation of productivity
with irradiance was studied using different incubation periods, from minutes to
hours. The influence of the exposure time on the P/I curve parameters was analysed. The results show that dissolved
oxygen concentration in the water does not increase linearly with time and that
PBmax and Iopt are
time-dependent. Exponential and linear expressions were proposed to describe PBmax and Iopt as a function of time. A
model was built to investigate the importance of static vs. dynamic simulation in the prediction of phytoplankton
production under different light intensities. The results show the importance
of using dynamic expressions for the P/I
relationship especially in mixed water column.
Key Words: biomass
concentration, phytoplankton productivity, short incubation periods, oxygen
method, ecological model.
Introduction
The photosynthesis-irradiance
(P/I) relationship is fundamental to
estimates of phytoplankton productivity. Several mathematical models have been
proposed for its description (e.g. Steele 1962, Jassby & Platt 1976, Platt
et al. 1980, Falkowski & Wirick 1981, Mergard et al. 1984, Eilers &
Peeters 1988, Pahl-Wostl & Imboden 1990, Janowitz & Kamykowski 1991).
These models can be divided into static and dynamic according to whether they
are steady state or time-dependent.
The dependence of photosynthesis on light intensity may be altered by
variations recently experienced by the organisms. The major source of these
fluctuations is vertical motion (Denman & Gargett 1983), which will not
only maintain the phytoplankton population in the mixed layer, but will also
have a profound effect on photosynthetic rates.
Short-term (minutes to hours) variation in phytoplankton physiology is a
general problem in the measurement and prediction of primary productivity in
mixed layers in estuaries. Whereas “in a continental shelf, with a photic zone
of 50 m and a vertical diffusion coefficient of about 50 cm2 s-1,
a phytoplanktonic cell crosses the photic zone and therefore the full gradient
of irradiance in the mixed layer in about 3 days, the same range of irradiance
is crossed in 13 minutes, in an estuary with a photic depth of 2 m” (MacIntyre
& Geider 1996). In turbid estuaries with shallow waters the photic zone may
be less than 0.5m deep, and the phytoplankton may be mixed through most of the
photic zone in 3 to 4 minutes (MacIntyre, 1993). Several workers have studied
the effect that fluctuations in the light field have on productivity (Marra
1978 a, b, Gallegos & Platt 1985, Yoder & Bishop 1985, Randall &
Day 1987, Mallin & Pearl 1992, Franks & Marra 1994, MacIntyre &
Geider 1996). There is some evidence that phytoplankton can maintain high rates
of photosynthesis during the first minutes after initial exposure to saturating
or inhibiting irradiance (Harris & Lott 1973, Harris & Piccinin 1977,
Marra 1978 a, b). The major concern is that photoinhibition is a time-dependent
process (Kok 1956, Takahashi et al.
1971, Harris & Lott 1973). During mixing, the residence time of
phytoplankton in the surface layer, where photoinhibition may occur, is of the
same order of magnitude as the time over which phytoplankton can maintain high
rates of photosynthesis before photoinhibition becomes prevalent. It is also
known that long period incubations (> 2 h) may lead to underestimation of
the photosynthetic rates (Lewis et al. 1984, Gallegos & Platt 1985,
Pahl-Wostl & Imboden 1990). Therefore the classical way of measuring
primary productivity by the light/dark bottle technique, and the use of the
results obtained to estimate the P-I
curve parameters might lead to overestimation of photoinhibition.
It is well established
that the parameters used in the productivity-light curve change as a result of
adaptation at different time scales, suggesting that the dynamic behaviour of
the P/I curve parameters should be
included in ecological models.
The problem of
determination of short-term processes in phytoplankton physiology is also a
problem concerning the methods used to estimate the photosynthetic and
respiration rates. The 14C method allows the measurement of carbon
fixation even at very low production rates, but artifacts which may arise when
using this method (measuring gross or net photosynthesis, use of radioactive
material, differential uptake of 14C/12C) are still a
matter of controversy (Peterson 1980, ICES 1996). The advantage of the oxygen method
is that net primary production (NPP), gross primary production GPP) and
respiration (R) may be determined. One of the disadvantages is that
heterotrophic respiration is also included in the measurement. More
importantly, the sensitivity of this method is usually too low to pick up
oxygen changes under short (< 1 h) incubation times. This question may be
addressed by concentrating the phytoplankton biomass, in order to reduce the
incubation period by increasing the consumption/production of carbon/oxygen
(Duarte & Ferreira 1997).
Experiments using
concentrated phytoplankton samples were performed by other authors to measure
the photosynthetic and/or respiration rates from natural populations (e.g.
Pomeroy & Johannes 1968, Harris & Piccinin 1977). The methodology of
concentration found in the literature is very variable, from the Dodson &
Thomas (1964) method, through centrifugation (e.g. Iwakuma & Yasuno 1983),
to the use of concentrating nets. The first two methods have long time procedures and/or allow only
the concentration of small volumes. On the other hand, nets are generally used
to quickly filter large volumes of water for taxonomic studies. The main
disadvantages of the nets are the potential distortion of species composition
due to phytoplankton selectivity, clogging in turbid waters, damage to some
organisms (particularly naked flagellates, UNESCO 1978) and inclusion of
zooplankton in the sample. In the present work, an alternative phytoplankton
concentration net was developed to concentrate large volumes of phytoplankton
rapidly without concentrating the zooplankton, clogging or damaging the
organisms. This net was tested in a very turbid water column.
Data collected by Marra (1978a, b), Marra &
Heinemann (1982) and Cullen & Lewis (1988) have been the basis of several
models that relate photosynthesis to fluctuating light intensity (Neale &
Marra 1985, Pahl-Wostl & Imboden 1990, Franks & Marra 1994). New data
for the relation of time dependence of P/I
relationship is presented and a different model for this relation is proposed.
The objectives of the present work are the following:
1)
To develop a technique that allows fast
phytoplankton pre-concentration and to explore the potential for short-term
photosynthetic measurements using the oxygen method;
2)
To use this technique to study short-term
photosynthesis-irradiance (P/I)
relationships;
3)
To investigate the influence of the exposure
time on the P/I curve parameters;
4)
To develop a primary production model that
takes into account the dynamic behaviour of the P/I curve parameters.
MAterial
and Methods
Study area. The Tagus Estuary
(Portugal) (Fig. 1) is a large estuarine ecosystem (surface area of 320 km2
and mean volume of 1900´106
m3 (Ferreira & Ramos 1989)). The tidal amplitude ranges from
less than 1 m to 4 m during a spring-neap cycle. The Tagus River is the main
source of freshwater to the estuary, with a modal discharge of about 400 m3.s-1.
This corresponds to an estuary number of less than 1%, indicating that the
system should in general be vertically well mixed, which is verified in the
field, although the circulation is not laterally homogenous (Carvalho et al. 1997).
Fig. 1. (near here)
The data were obtained in a channel of the Tagus estuary, with a mean
depth of 2.3 m. The salinity ranges from 0 to 32 psu and is strongly influenced
by the semi-diurnal and fortnightly tidal cycles. The water is very turbid,
with annual values of suspended matter ranging from 45 mg.l-1 to
120 mg.l-1.
Sampling and treatment. The
experiments were performed over a period of six weeks (May-July, 1996) when the
biomass of planktonic algae was consistently high, with chlorophyll-a (Chl a) concentrations varying from 8 to 47
mg Chl a m-3. Surface water samples for the
determination of physical and chemical parameters and phytoplankton biomass
were taken hourly over 3 to 5 hours, depending on the experiment. Temperature,
oxygen, salinity and light extinction were measured in situ. The phytoplankton biomass was concentrated using a net
built with the aim of rapidly concentrating large volumes of phytoplankton in a
turbid water column. This net consisted of 3 filtering cones with different
gauze (200 mm, 41 mm and 15 mm) nested inside each other: the first, with 200 mm, did not have a plankton-collecting vessel and was used to restrict
the input of detritus and zooplankton (Fig. 2). The water inflow was reduced by
the small diameter of the mouth ring and by the non-porous textile cone in
front of the net. This modification increased the ratio between the filtering
area and the mouth area and reduced clogging.
Fig. 2. (near here)
After towing, the net
was washed with estuarine water, previously filtered through a 15 mm filter. The plankton was collected from sampling flasks connected to
the 41 and 15 mm nets. The filtered water (< 15 mm) was also used as a control sample. All samples were kept in darkness
(4 hours) until incubation. The time spent by the phytoplankton cells in the
dark was identical in all the experiments.
Species determination.
Concentrated, non-concentrated and control samples for species determination
were preserved with Lugol’s solution. Phytoplankton cells were counted by the
Utermöhl technique. Cell abundance data were transformed into relative values
of species biomass, through the Taguchi equation (Taguchi, 1976) using cell
volumes reported in the literature (Jørgensen et al. 1991).
Incubation procedures. Samples
were incubated in the laboratory using light provided by 1500 W tungsten
halogen lamps. Heat produced by the lamps was dissipated using a cold water
flow system. Light intensity (0 to 1445 mE m-2 s-1) was measured by a LI-COR underwater
cosine quantum sensor and attenuation was achieved by means of grey PVC nets.
Preservation of the spectral characteristics was verified by spectral analysis
(Fig. 3). Three replicate Winkler flasks (65 ml), volume calibrated to 0.01 ml,
were incubated for each light intensity, for periods ranging from 15 to 240
minutes.
Fig. 3. (near here)
Chemical analyses. Concentration
of oxygen was measured in replicate bottles by titration with the azide
modification of the Winkler method (Phillips 1973). A microburette was used to
titrate the whole contents of the Winkler bottles (Carritt & Carpenter 1966,
Strickland & Parsons 1972). Chlorophyll-a concentration was determined
fluorometrically by the method of Yentsch & Menzel (1963) as modified by
Holm-Hansen et al. (1965).
Primary production determination. Productivity and respiration were measured from oxygen differences by
the light-dark bottle technique. A photosynthetic quotient of 1.2 and a
respiratory quotient of 0.8 were used in the conversion of oxygen to carbon
according to Vollenweider (1974) and Geider & Osborne (1989). Three
different experiments were performed for primary production determination.
The purpose of the
first experiment (experiment I) was to test whether the rate of oxygen
production or respiration was affected by the pre-concentration technique of
the phytoplankton biomass. A concentrated phytoplankton sample was diluted with
a control sample to obtain different concentrations. All samples were incubated
at 100 mE m-2 s-1 for a period of 240 minutes.
The aim of experiment
II was to study the P/I relationships
in a natural phytoplankton sample. The incubation was performed with a
non-concentrated sample but some phytoplankton was also concentrated for
species determination. The samples were incubated for 3 hours at light
intensities ranging from 0 to 1280 mE m-2
s-1. Since the choice of different P/I models frequently leads to different estimated parameter values
of the P/I curve (Frenette et al., 1993), three different models
were used (Table 1). The superscript B
denotes that P/I characteristics were
calculated per mg chlorophyll-a.
Table 1. (near here)
Some of the P/I curve parameters cannot be derived
directly from the equations shown in Table 1, therefore some additional
calculations were performed. The Iopt
(optimal light intensity) and PBmax
(maximal production rate) can be directly obtained from Steele’s (1965)
equation. The initial slope of the light saturation curve (a)
can be determined by
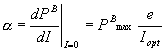 (mgC mgChl a-1
h-1 mE-1 m2 s) (1)
(mgC mgChl a-1
h-1 mE-1 m2 s) (1)
The ratio, PBmax:
a ,
is identical to the parameter Ik
defined by Talling (1957) and corresponds to the point at which the linear part
of the light-saturation curve intersects the plateau.
The parameters a, b, and PBs
directly result from the Platt et al. (1980)
model. According to the authors the Iopt
parameter can be obtained by
![]() (mE m-2 s-1) (2)
(mE m-2 s-1) (2)
and substituting (2) in the Platt et al. (1980) equation (Table 1) gives
the maximum productivity
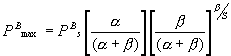 (mgC mgChl a-1
h-1) (3)
(mgC mgChl a-1
h-1) (3)
When the photoinhibition parameter (b) tends to zero, PBs tends to PBmax, that is PBmax and PBs coincide if
there is no inhibition.
By differentiating the
Eilers & Peeters (1988) model (Table 1) the parametersa, PBmax and Iopt can be expressed as a
function of the a, b, and c parameters:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
and, according to the previous authors, the reverse equations are
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
In the last experiment (experiment
III) three replicates of concentrated samples were incubated at different light
intensities, from 0 to 1445 mE m-2
s-1 using four incubation periods: 15, 45, 90 and 180 minutes. The
influence of exposure time on the P/I
curves and parameters was determined. The maximum rate of photosynthesis, PBmax, and the
optimal light intensity, Iopt,
were described as time-dependent according to the results found in this
experiment.
Model development. A
productivity function dependent on light intensity and incubation time (P(I,t)) was developed from the Eilers
& Peeters model in order to account for the dynamic aspects of the P/I relationships. A simple mathematical
model was built using this productivity function, and assuming a respiration
rate constant over the time equal to the value determined experimentally. The
only biological state variable was phytoplankton and other processes such as
nutrient or temperature limitation, were not considered. Primary productivity
modelling was carried out by means of static and dynamic formulations. The only
difference between these two models is the definition of the productivity
function. In the dynamic model the function P(I,t)
was used and the parameters changed as a function of the time. In the static
model the Eilers & Peeters (1988) P(I)
function was used and the parameters remained constant over the simulation
period. A time step of 0.1 minutes was used in the simulations. Productivity
was expressed as mgO2 mg
Chla-1 min-1
and the parameter a was used to calibrate the model.
Results
and discussion
A summary of the physical and chemical parameters and chlorophyll-a
concentration determined during sampling is presented in Table 2. The
chlorophyll-a concentration observed in the field during these experiments was
consistently high, which can be related to the sampling season (spring-summer).
Data from previous studies (Moita, 1982; Macedo, 1997) reported that
phytoplankton biomass in the same area can range from 0.1 to 39 mg Chl.a m-3.
Table 2. (near here)
The concentration
procedure allowed the concentration of the phytoplankton biomass from a sample
with high concentration of suspended particulate matter. It took about 4 hours
to collect volumes of 5 to 10 l of concentrated sample. The relative biomass
values of the main species found in the concentrated (> 15 mm), non-concentrated (natural population) and control (< 15 mm) samples are presented in Fig. 4. These samples consisted mainly of
diatoms. Fragilaria cretonensis was
the most abundant species in the concentrated samples, accounting for more than
50% of the total biomass. In the natural (non-concentrated) and control samples
F. cretonensis only dominate in the
data from experiment I. In the other two experiments the most abundant species
were Chaetoceros sp. and Skeletonema costatum, which constituted
more than 60% of the natural and control samples. From these experiments it
appears that the concentration procedure increases the relative biomass value
of the species F. cretonensis.
Fig. 4. (near here)
It is important to note that the maximal concentration factor
(concentrated biomass/non-concentrated biomass) was about 20, in the first
experiment, and that a smaller concentration factor, about 3, was found in the
other two experiments. This is related to the fact that filtering properties of
a net are in part determined by the species composition of the plankton. When
chain-forming species (e.g. Skeletonema
costatum) or species with spines or setae (e.g. Chaetoceros spp.) are abundant in the natural sample the plankton
itself may form a network inside the gauze preventing a high concentration
factor (UNESCO, 1978). The number of damaged organisms found was very small,
and there was no apparent relation between this number and sample concentration.
However it is difficult to ascertain whether a significant number of organisms
can be destroyed by the use of this concentration net, because most of the
phytoplankters identified were diatoms.
In experiment I the effect of the biomass pre-concentration on the rate
of oxygen production and respiration was analysed. The results show that the
production and consumption of oxygen were linearly correlated with the increase
in Chl a concentration (ANOVA
p<0.05 and ANOVA p<0.01, respectively) (Fig. 5).
Fig. 5. (near here)
It was not possible to
measure the respiration rate when the chlorophyll-a concentration was below 45
mg m-3. From these results it appears that concentrating the
phytoplankton biomass does not affect specific oxygen production and
consumption rates.
In experiment II
natural phytoplankton samples were exposed to different light intensities. The
GPP values obtained were fitted to three different mathematical models (Fig. 6)
and the P/I parameters were derived
after fitting the data to these models using least-squares non-linear
regression.
Fig. 6 and Table 3 (near here)
The equations of Platt et al. (1980) and Eilers & Peeters (1988)
have a better fit than Steele’s (1965) equation. The Eilers & Peeters
(1988) model was chosen since it is based on the physiology of photosynthesis.
In experiment III
concentrated water samples were exposed to five different light intensities for
15, 45, 90 and 180 minutes. Fig. 7 shows the oxygen evolution over time at the
light levels tested. The dissolved oxygen concentration in the water does not
increase linearly with time, and at all the light intensities tested the slope
is higher for the initial exposure time. It is also noted that for incubation
periods longer than 45 minutes the oxygen evolution increases linearly with
time, except for the results under highest light intensity.
Fig. 7. (near here)
From these data it
appears that productivity is not just dependent on light intensity but also dependent
on exposure time, as reported by several authors (e.g. Marra 1978, Neale &
Marra 1985, Falkowski & LaRoche 1991, Franks & Marra 1994). As the
oxygen production does not increase linearly with time, the production rate is
not constant, and cannot be estimated as the difference between the final and
the initial value of oxygen concentration. To overcome this problem, the gross
production rates were calculated for the partial time intervals (0-15; 15-45;
45-90 and 90-180). The respiration rate was determined using 180 minutes of
dark incubation. Since there was no data on respiration from shorter incubation
periods, a constant respiration rate was assumed. The values obtained were
fitted using the Eilers & Peeters’ (1988) equation (Fig. 8 and Table 4).
Fig. 8. and Table 4 (near here)
This study was
performed during early summer in a temperate zone. The high values of
phytoplankton biomass shown in Table 2 reflect a well-known seasonal trend,
with high values in spring-summer and low values in winter (Moita 1982, Cabrita
& Moita 1995, Macedo, 1997). These biomass values are also a reflection of
the considerable primary production rates occurring during this season. In
fact, the PBmax
values found, for incubation periods longer than 45 minutes (Table 4), fall in
the upper range of the representative values, from 0.2 to 17 mg C mg Chl a-1 h-1, proposed
by Lalli & Parsons (1993). For shorter incubation periods the PBmax values
reported were even higher. Table 5 presents maximal production rates of phytoplankton
populations from different sites. From this table it can be seen that the
maximum primary production values exhibit a very broad range.
The respiration rate found in this experiment ( 1.8 mg C mg Chl a -1 h-1) ranged
from 5% to 19% of the PBmax
value, depending on the incubation interval. This relation, R/Pbmax, falls
within commonly quoted values, i.e. between 5 and 20 %.
From Fig. 8 it can be
seen that short-time incubation resulted in a saturation curve instead of an
inhibition curve. Photoinhibition needs time to develop and become measurable
(Kok 1956, Harris & Piccinin 1977, Marra 1978 a, b, Belay 1981, Whitelam
& Codd 1983). For short incubations, after the phytoplankton was kept in
the dark, all the “photosynthetic factories” (sensu Crill 1977) are in the resting state: When the cells are
subsequently exposed to light, the equilibrium between the resting state and
the activated state will settle fast (Eilers & Peeters 1988, 1993). This
means that in a short incubation period there will be very few transitions from
the activated state to the inhibited state, whereas when light intensity
remains very high for a long time photoinhibition becomes progressively more
important.
The photosynthetic rate
decreases with time for all irradiance levels as can be seen from the plot in
Fig. 9. The greatest absolute reduction occurs at the higher light intensities;
however, the greatest relative decrease happens at lower irradiances. The
results follow a similar pattern to the ones observed experimentally by Marra
(1978) and predicted by the DYPHORA model (Pahl-Wostl & Imboden 1990).
However in Marra's (1978) data, for irradiance levels lower than or equal to
150 mE m-2 s-1, the curve does not show a decrease with
time. Since our data (Fig. 9) have only one light level above this value its
not possible to predict if the photosynthetic rate will fallow the same pattern
for any given light intensity above 100 mE m-2 s-1.
Fig. 9. (near here)
In the present study a light inhibition decay time of about 1 to 2 hours
was found. This value falls in the range predicted by Pahl-Wostl & Imboden
(1990). The critical light intensity for onset of light inhibition must be
below 100 mE m-2 s-1, since for all the light intensities
tested the exposure time has influence on the production rates.
From the previous
results it seems that all the P/I
curve parameters are time-dependent. In some experiments it has been observed
that after prolonged illumination with strong light, both PBmax and the initial slope are reduced (Kok
1956, Steeman-Nielsen 1962). Neale & Marra (1985) pointed out that the
variation of PBmax should be considered as the primary source of
time-dependence and Franks & Marra (1994) present a non linear
time-dependent PBmax.
A decrease in the Iopt
with time was also observed for light intensities higher than the critical
value. Henley (1993) gives examples of experiments conducted by other authors
where a reduction in a
occurs before any detectable change in PBmax.
Such a decrease is not clear from the data presented, since the minimal light
intensity used, 100 mE m-2 s-1, is too high for initial slope
evaluation. Therefore only the PBmax
and Iopt parameters were
assumed to be time-dependent. The variation of PBmax and Iopt
with exposure time was analysed considering the centre of each time interval
(Fig. 10).
Fig. 10. (near here)
The parameter Iopt decreases linearly with
incubation time. The maximum production rate, PBmax, can be related to time by a negative
exponential function, that reduces the PBmax
until a constant lower value. This indicates that if phytoplankton is exposed
to a critical irradiance for a short period of time, primary productivity may
be higher than expected when measured for the same light intensity, after the
incubation of phytoplankton for a period of a few hours. However, this relation
implies an extremely high PBmax
value when the exposure time is zero, which is obviously false. In fact this
equation predicts that, for small incubation periods, the PBmax values increase with the decrease of
the incubation time. But the experiments were performed until a minimum time of
15 minutes, so prediction of values to lower incubation times would be an extrapolation.
According to several authors (e.g. Harris & Piccinin 1977, Pahl-Wostl &
Imboden 1990) a rapid increase in productivity, starting from zero, should be
expected until the cells reach their full rate of photosynthesis, which must
occur after 0.5 to 5 minutes. This rapid increase in the photosynthesis during
the first few minutes is probably due to the activation of Rubisco (MacIntyre
& Geider 1996). According to these authors the rate at which photosynthesis
is induced and reduced, due to increase and decrease of the irradiance, is
limited by the kinetics of Rubisco’s activation and deactivation. Therefore,
these equations can only be used within the period tested
A time-dependent model
for the P/I relationship was
developed from the Eilers & Peeters model. Using equation (7) and (8) and
the relation found for the PBmax
and Iopt varying with
time, the following relation was established:
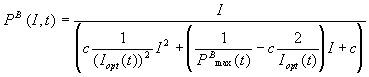 (mgO2 mgChl
a-1 min-1) (10)
(mgO2 mgChl
a-1 min-1) (10)
where the production rate is dependent on the light intensity and also
on time.
Using equation (10) for
the oxygen production rate a model for the calculation of the dissolved oxygen
was built. The model was conceptualised as simply as possible, to investigate
solely the importance of dynamic behaviour of oxygen production under different
light intensities. The conceptual diagram of this model and the corresponding
equations are presented in Fig. 11 and Table 6.
Table 6 and Fig. 11 (near here)
The relation between
oxygen concentration predicted by this model and the observed data can be seen
in Fig. 12. The simulation results indicate that the productivity function, PB(I,t), and the respiration
rate used are adequate to describe the observed variation in oxygen
concentration during the experiments.
Fig. 12. (near here)
If the productivity
were determined solely from an incubation period of 0 to 180 minutes it would
be accepted that the oxygen production increases linearly with time and
productivity would be described as a static function, meaning that PBmax and Iopt values should be
constant for any given time. In Fig. 13, the results obtained for static and
dynamic simulations are compared and evaluated in the light of existing data.
Fig. 13. (near here)
As expected, the static
model matches the observed values well when the 180 minute curve is used. For
incubation periods shorter than 180 minutes the static model underestimates the
oxygen concentration. This underestimation is quite significant since the
values predicted by the static model for 45 minutes are very close to the
values observed at 15 minutes, the same occurring for the 90-minute static
curve, which passes near the values determined at 45 minutes of incubation
time. When strong vertical turbulence occurs, the time taken by a given phytoplanktonic
cell to traverse the full gradient of irradiance, in a 2 m water column, is
less than 180 minutes and the static formulation is far from the real data.
This model gives a dynamic description of photosynthesis and
photoinhibition using only three parameters that can be easily deduced from any
P/I curve. The PBmax(t)
and Iopt(t) equations are
represented by simple equations (exponential and linear) which may be fitted to
other set of data. Furthermore this model was based on a rational model of the
photosynthesis. One of its disadvantages is the assumption of a constant value
for a, which is probably not the most realistic approach. Another constraint
is the absence of a parameter for the light activation of photosynthesis as
described by other authors, e.g. Pahl-Wostl & Imboden (1992) and MacIntyre
& Geider (1996). This parameter was not be implemented because the time
resolution of our experimental data was not high enough to estimate the
activation time.
Concluding
Remarks
The main conclusion emerging from the simulations performed is that the
dynamic behaviour of the production-light curves is relevant in the simulation
of primary productivity, and that this is accentuated when short-term
production is determined. Oxygen evolution through time was found to be
non-linear and the parameters PBmax
and Iopt are
time-dependent. Short-term (minutes to hours) variation in phytoplankton
physiology is a general problem in the measurement and prediction of primary productivity
in the surface mixed layer. When vertical mixing is considered, photoinhibition
may be present at higher depths than without mixing, although surface
inhibition is weaker than when mixing is absent. This is due to the downward
transport of partially or fully inhibited cells (Duarte & Ferreira, 1997).
The results show the importance of redesigning the way primary productivity is
usually measured by incubating water samples with phytoplankton for several
hours at fixed depths.
The concentration procedure used in this study allowed the measurement
of production rates by the oxygen method during short incubation periods. This
method is easy to implement, less expensive than the radioactive carbon method
and allows the calculation of the gross primary production and respiration. The
use of this particular design of net has also the advantage of decreasing the
errors due to zooplankton respiration. From the results presented in this study it appears that concentration does not
affect the production or respiration rates. However the specific diversity and
the species composition can be more or less affected by the concentration
procedure depending on the species assemblage present. Further research needs
to be done in order to improve and test this concentration methodology, but the
results obtained are encouraging. This methodology can be very useful for
primary production studies, particularly in areas of low productivity, for
size-fractionation studies and short-term oxygenic photosynthesis studies, or
when radioactive carbon cannot be used.
Acknowledgements
This research was supported by PRAXIS XXI Program (M. Sc. grant
BM/534/94), the ECOTEJO project (JNICT PBIC/C/MAR/1293/92) and by SOLVAY -
Portugal. We thank F. J. Pina (New University of Lisbon) for helpful
discussions and for making laboratory facilities available and P. Mendes for
species composition analysis. The authors are also grateful to four anonymous
referees for comments and helpful suggestions.
LITERATURE CITED
Belay A (1981) An experimental investigation of
inhibition of phytoplankton photosynthesis at lake surfaces. New Phytol
89:61-74
Cabrita
MT, Moita MT (1995) Spatial and temporal variation of physico-chemical
conditions and phytoplankton during a dry year in the Tagus Estuary (Portugal).
Neth Journal of Aquat Ecol, 29(3-4): 323-332.
Carritt DE, Carpenter JH (1966). Comparison and evaluation of
currently employed modifications of the Winkler method for determining
dissolved oxygen in seawater; A NASCO Report J mar Res 24(3):286-318
Carvalho ML, Ferreira JG, Amorim P, Marques
MIM, Ramos MT (1997) Study of heavy metals and other elements in macrophyte
algae using energy-dispersive X-ray fluorescence. Environ Toxicology &
Chemistry 16(4): 807-812.
Côté B, Platt T (1983) Day-to-day variations in
the spring-summer photosynthetic parameters of coastal marine phytoplankton.
Limnol Oceanogr 28 (2): 320-344.
Crill PA (1977) The photosynthesis-light curve:
a simple analogue model. J Theor Biol 6:503-516
Denman
KL, Gargett AE (1983) Time and space scales of vertical mixing and advection of
phytoplankton in upper ocean. Limnol Oceanogr 28(5):801-815.
Dondson
AN, Thomas WH (1964) Concentrating plankton in a gentle fashion. Limnol
Oceanogr 9(3):455-456
Duarte P, Ferreira JG (1997) Dynamic Modelling
of photosynthesis in Marine and estuarine ecosystems. Env Model and Assess
2:83-93
Eilers
PHC, Peeters JCH (1988) A model for the relationship between light intensity
and the rate of photosynthesis in phytoplankton. Ecol Model 42:199-215
Eilers PHC, Peeters JCH (1993) Dynamic
behaviour of a model for photosynthesis and photoinhibition. Ecol Model
69:113-133
Falkowski PG, Wirick CD (1981) A simulation
model of the effects of vertical mixing on primary productivity. Mar Biol
65:69-75
Falkowski PG, LaRoche J (1991) Minireview.
Acclimation to spectral irradiance in algae. J Phycol 27:8-14
Ferreira JG, Ramos L (1989) A model
for the estimation of annual production rates of macrophyte algae. Aqua Bot
33:53-70
Franks PJS, Marra J (1994) A simple
new formulation for phytoplankton photoresponse and an application in a
wind-driven mixed layer. Mar
Ecol Prog Ser 111:143-153
Frenette
JJ, Demers S, Legendre L, Dodson J (1993) Lack of agreement among models for
estimating the photosynthetic parameters. Limnol Oceanogr 38(3):679-687
Gallegos CL, Platt T (1985) Vertical advection
of phytoplankton and productivity estimates: a dimensional analysis. Mar Ecol Prog Ser 26:125-134
Geider RJ, Osborne BA (1989) Respiration and
microalgal growth: a review of the quantitative relationship between dark
respiration and growth. New Phytol 112:327- 211
Harris GP, Lott JNA (1973) Light intensity and
photosynthetic rates in phytoplankton. J Fish Res Bd Can 30:1771-1778
Harris GP, Piccinin BB (1977) Photosynthesis by
natural phytoplankton populations. Arch Hydrobiol 59:405-457
Henley WJ (1993) Measurement and interpretation
of photosynthetic light-response curves in algae in the context of
photoinhibition and diel changes. J Phycol 29:729-739
Holm-Hansen
O, Lorenzen CJ, Holmes RW, Strickland JDH (1965) Fluorometric determination of
chlorophyll. J Cons Int Explor Mer 30:3-15
ICES CM (1996)/L:3. Biological Oceanography
Committee. Report of the working group on phytoplankton ecology. Ref: C+E+Env 28-30.
Iwakuma T, Yasumo M (1983) Comparison of
several mathematical equations describing photosynthesis-light curve for
natural phytoplankton populations. Arch Hydrobiol 97(2):208-226
Janowitz GS, Kamykowski D (1991) An
Eulerian model of phytoplankton photosynthetic response in the upper mixed
layer. J Plankton Res 13(5): 988-1002
Jassby
AD, Platt T (1976) Mathematical formulation of the relationship between
photosynthesis and light for phytoplankton. Limnol Oceanogr 21(4):540-547
Jørgensen SE, Nielsen SN, Jørgensen
LA (1991) Handbook of ecological parameters and ecotoxicology. Elsevier,
London.
Kok
B (1956) On the inhibition of photosynthesis by intense light. Biochim Biophys
Acta 21:234-244
Kromkamp
J, Peene J (1995) Possibility of net phytoplankton primary production in the
turbid Schelde Estuary (SW Netherlands). Mar Ecol Prog Ser, 121: 249-259.
Lalli
CM, Parsons TR (1993) Biological Oceanography: An Introduction.
Butterworth-Heinemann Ltd, Oxford
Lewis
MR, Cullen JJ, Platt T (1984) Relationships between vertical mixing and
photoadaptation of phytoplankton: similarity criteria. Mar Ecol Prog Ser 15:141-149
Macedo MF (1997) Simulação da produtividade
primária fitoplanctónica. Aplicação à Cala do Norte do Estuário do Tejo. M. Sc.
Thesis. Faculty of Sciences
and Technology, New University of Lisbon
MacIntyre S (1993) Vertical mixing in a shallow
eutrophic lake: possible consequences of the light climate of phytoplankton.
Limnol Oceanogr 38:798-817
MacIntyre HL, Geider RJ (1996) Regulation of
Rubisco activity and its potential effect on photosynthesis during mixing in a
turbid estuary. Mar Ecol Prog
Ser 144:247-264
Mallin MA, Pearl HW (1992) Effects of variable
irradiance on phytoplankton productivity in shallow water. Limnol Oceanogr
37:54-63
Marra
J (1978a) Effect of short-term variations in light intensity on photosynthesis
of marine phytoplankter: A laboratory simulation study. Mar Biol 46:191-202
Marra
J (1978b) Phytoplankton photosynthetic response to vertical movement in mixed
layer. Mar Biol 46:203-208
Mergard RO, Tonkyo DW, Senft WH
(1984) Kinetics of oxygenic photosynthesis in planktonic algae. J Plankton Res
6(2):325- 337
Moita MT (1982) Estudo ambiental do Estuário do
Tejo. Estudos dos pigmentos (clorofila a
e feopigmentos) colhidos no estuário do Tejo em 1980. CNA/TEJO nº15, Rel. 14:
1-185.
Neale
PJ, Marra J (1985) Short-term variation of Pmax under natural irradiance
conditions: a model and its implications. Mar Ecol Prog Ser 26:113-124.
Pahl-Wostl
C, Imboden DM (1990) DYPHORA - a dynamic model for the rate of photosynthesis
of algae. J Plankton Res 12:1207-1221
Peterson
BJ (1980) Aquatic primary productivity and the 14C-CO2
method: a history of the productivity problem. A Rev Ecol Syst 11:359-389
Phillips
JA (1973) Winkler method and primary production studies under special
conditions. In: A guide to the measurement of marine primary production under
some special conditions. UNESCO
Paris, p 48-54
Platt
T, Gallegos CL, Harrison WG (1980) Photoinhibition of photosynthesis in natural
assemblages of marine phytoplankton. J mar Res 38:687-701
Pomeroy
LR, Johannes RE (1968) Occurrence and respiration of ultraplankton in the upper
500 meters of the sea. Deep-Sea Res 15:381-391
Randall
JM, Day JW (1987) Effects of river discharge and vertical circulation on
aquatic primary production in a turbid Louisiana (USA) estuary. Neth J Sea Res
21:231-242
Riegman
R, Colijn F (1991) Evaluation of measurements and calculation of primary
production in the Dogger Bank area (North Sea) in Summer 1988. Mar Ecol Prog Ser 69: 125-132.
Savidge
G (1988) Influence of inter- and intra-daily light-field variability on
photosynthesis by coastal phytoplankton. Mar Biol 100:127-133
Steele JH (1962) Environmental control of
photosynthesis in the sea. Limnol Oceanogr 7:137-150
Steemann Neilsen E (1962) Inactivation of the
photochemical mechanism in photosynthesis as a means to protect cells against
high light intensities. Physiol Plant 15:161-171
Strickland JDH, Parsons TR (1972). A practical
handbook of sea water analysis. 2nd Ed Bull Fish Res Bd Can 167
Taguchi S. (1976) Relationships between
photosynthesis and cell size of marine diatoms. J Phycol 12(2):185-189
Takahashi M, Shimura S, Yamaguchi Y, Fujita Y
(1971) Photoinhibition of phytoplankton photosynthesis as a function of the
exposure time. J Oceanogr Soc
Japan 27:43-50
Talling JF (1957) Photosynthetic
characterisation of some freshwater plankton diatoms in relation to underwater
radiation. New Phytol 56:29-50.
UNESCO (1978) Phytoplankton manual. Ed. A. Sournia.
Muséum National d´histoire Naturelle, Paris
Vollenweider RA (1974) A manual on methods for
measuring primary productivity in aquatic environments. Blackwell Scientific
Publications, Oxford
Whitelam GC, Codd GA (1983) Photoinhibition of
photosynthesis in the cyanobacterium Microcystis
aeroginosa. Planta 157:561-566
Yentsch
CS, Menzel DW (1963) A method for the determination of phytoplankton
chlorophyll and phaeophytin by fluorescence. Deep Sea Res 10:221-231
Yoder JA, Bishop SS (1985) Effects of mixing-induced
irradiance fluctuations on photosynthesis of natural assemblages of coastal
phytoplankton. Mar Biol 90:87-93
Figures
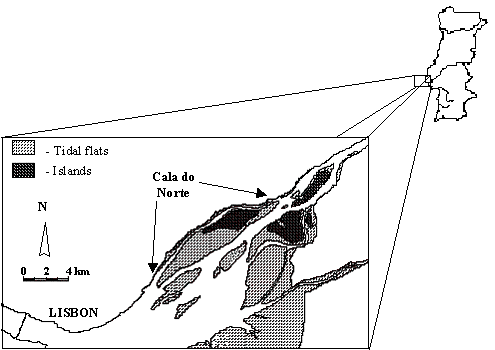
Fig. 1. Cala do Norte of the Tagus Estuary.
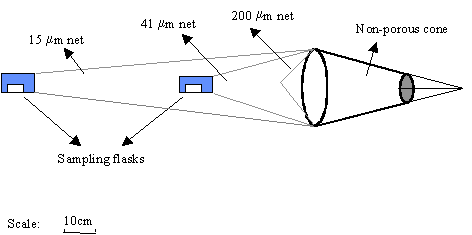
Fig. 2. Towing net used to concentrate phytoplankton.
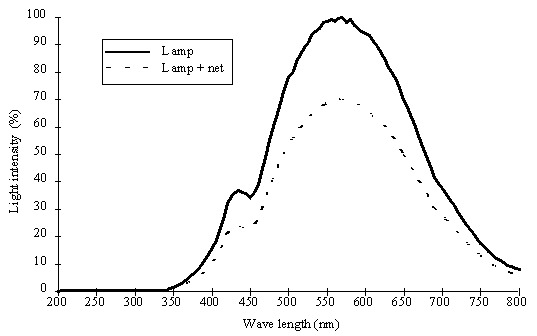
Fig. 3. Direct emission spectra of the tungsten halogen lamp and through
the PVC net.
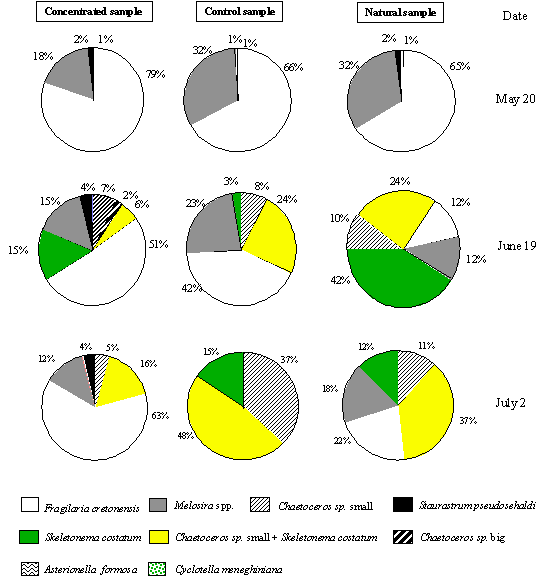
Fig. 4. Relative percentage of the main taxonomic groups found in the
concentrated, non-concentrated and control samples.
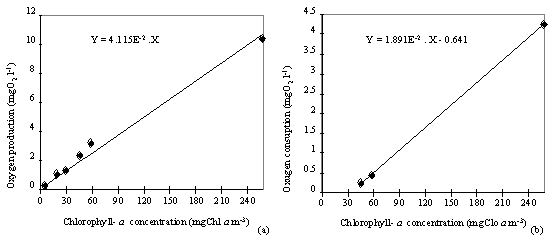
Fig. 5. Relation between the
chlorophyll-a concentration and the
oxygen production (a) and consumption (b), obtained from experiment I. Each
point represents the mean value of three replicates.
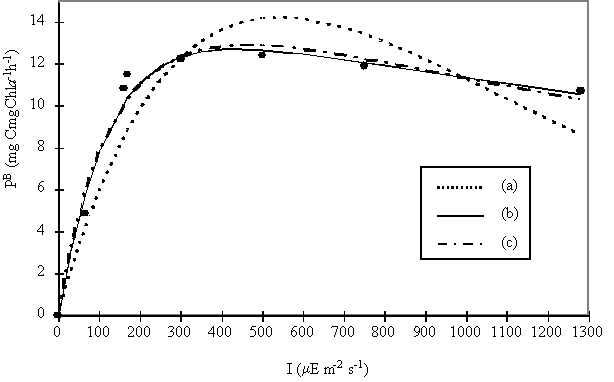
Fig. 6. Photosynthesis versus Irradiance (P/I) curves obtained after fitting the data with the Steele (1965)
(a), Platt et al. (1980) (b) and Eilers & Peeters (1988) (c) equations.
Each point represents the mean value of three replicates obtained from a
non-concentrated sample.
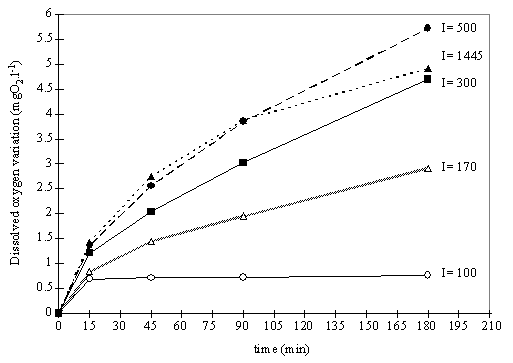
Fig. 7. Variation of the dissolved oxygen concentration during the incubation
period at five different light intensities. Each point represents the mean
value of three replicates obtained from a concentrated sample.
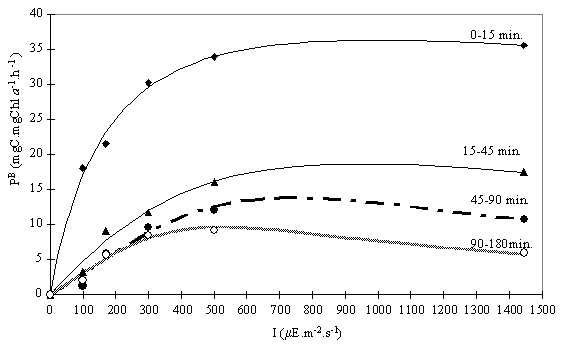
Fig. 8. Average productivity calculated from the time intervals 0-15;
15-45; 45-90; 90-180 minutes. The P/I
curves were obtained after fitting the data from different incubation times,
with the Eilers & Peeters (1988) model. Each point represents the mean
value of three replicates obtained from a concentrated sample.
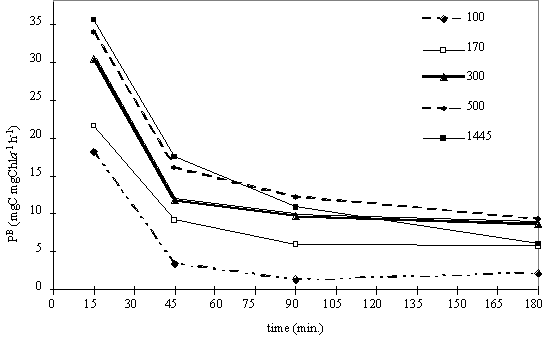
Fig. 9. Variation of production rate over time at five light levels.
Each point represents the mean value of three replicates obtained from a
concentrated sample.
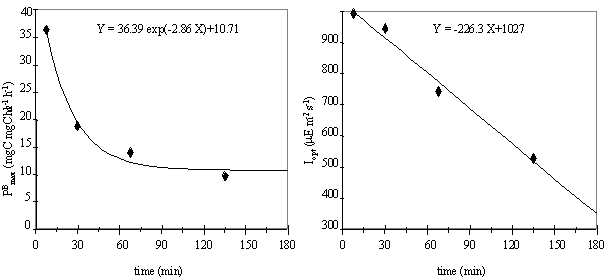
Fig. 10. Variation of PBmax
and Iopt with the exposure
time.
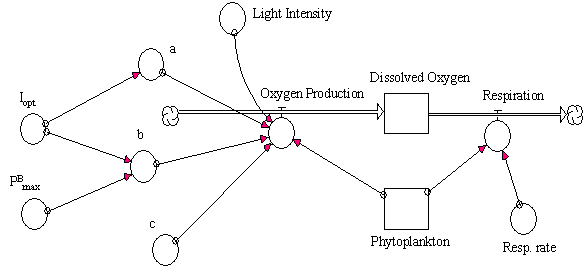
Fig. 11. Conceptual diagram of the dynamic dissolved oxygen model.
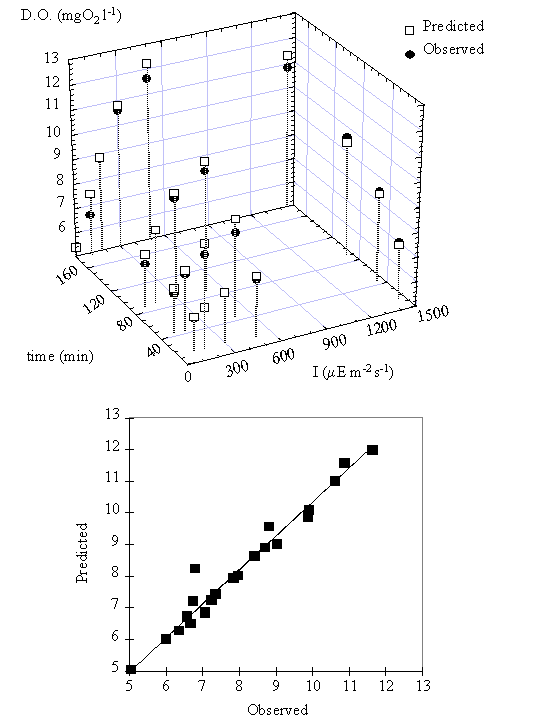
Fig. 12. Predicted () and observed (l)
values of the dissolved oxygen concentration. The slope of the regression line
between observed and predicted values is not significantly different from 1 and
the y-intercept is not significantly different from 0 (p < 0.05).
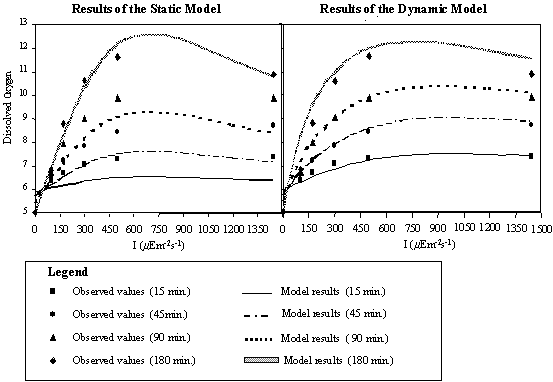
Fig. 13.
Dissolved oxygen values predicted by the dynamic and static models plotted
against the observed values.
Tables
Table 1. Equations used to calculate the photosynthesis-irradiance (P/I) parameters. Where I is the light intensity, Iopt is the optimal light intensity, PBmax is the
maximal production rate, b is the photoinhibition parameter and
a is the initial slope of the
light saturation curve.
|
Source |
Equation |
Type |
|
Steele (1965) |
|
Empirical |
|
Platt et al. (1980) |
|
Empirical |
|
Eilers & Peeters (1988) |
|
Rational |
Table 2. Summary of the physical and chemical parameters and chlorophyll-a
concentration determined for the sampling dates.
|
Date |
Water temperature |
Dissolved oxygen |
Salinity |
Extinction coefficient (k) |
Chlorophyll-a |
|
(1996) |
(ºC) |
(mgO2.l-1) |
(psu) |
(m-1) |
(mg.m-3) |
|
May 20 |
16.5 |
6.2 |
0 |
4.86 |
7.7 |
|
May 20 |
16 |
6.8 |
0 |
6.8 |
13.1 |
|
May 20 |
16 |
7.2 |
0 |
6.8 |
14.3 |
|
May 20 |
16 |
6.9 |
0 |
6.8 |
13.3 |
|
May 20 |
16 |
6.9 |
0 |
5.7 |
10.6 |
|
June 15 |
24 |
nd |
nd |
nd |
46.6 |
|
June 19 |
23 |
4.5 |
21 |
3.4 |
22.8 |
|
June 19 |
23.5 |
4.5 |
16 |
3.4 |
14.6 |
|
June 19 |
25 |
5.2 |
10.5 |
4.25 |
16.9 |
|
June 19 |
25 |
5.6 |
8.5 |
4.86 |
17.8 |
|
June 19 |
25 |
6.0 |
8.0 |
4.86 |
19.0 |
|
July 2 |
21.5 |
8.5 |
24.5 |
6.8 |
21.7 |
|
July 2 |
22 |
8 |
19 |
5.7 |
23.6 |
|
July 2 |
22.5 |
8 |
9.5 |
6.8 |
19.9 |
|
July 2 |
23.5 |
7.8 |
8 |
5.7 |
19.1 |
|
July 2 |
24.5 |
7.5 |
14 |
4.86 |
23.4 |
|
July 2 |
24 |
5.8 |
19 |
4.25 |
27.5 |
nd: not determined
Table 3. Parameters of the P/I
curve obtained after fitting the data to the Steele (1965), Platt et al. (1980)
and Eilers & Peeters (1988) equations: a, the initial slope of the light saturation curve (mgC mgChl a-1 h-1 mE-1 m2 s), PBmax,
the maximal production rate (mgC mgChl a-1
h-1), the Iopt ,
optimal light intensity and Ik
light-saturation parameter (mE m-2
s-1).
|
Parameters of the P/I curves |
Steele (1965) |
Platt et al. (1980) |
Eilers & Peeters
(1988) |
|
a |
0.071 |
0.118 |
0.12 |
|
PBmax |
14.2 |
12.72 |
12.89 |
|
Iopt |
544 |
433 |
565 |
|
Ik |
200 |
108 |
103 |
|
ANOVA |
p > 0.05 |
p < 0.05 |
p < 0.05 |
Table 4. Parameters
of the P/I curve, for different
incubation periods, obtained after fitting data to the Eilers & Peeters
(1988) model: a, the initial slope of the light
saturation curve (mgC mgChl a-1
h-1 mE-1 m2 s), PBmax,
the maximal production rate (mgC mgChl a-1
h-1), the Iopt ,
optimal light intensity and Ik
light-saturation parameter (mE m-2
s-1).
|
Incubation period (min) |
0 - 15 |
15 - 45 |
45 - 90 |
90 - 180 |
|
a |
0.259 |
0.052 |
0.029 |
0.03 |
|
PBmax |
36.3 |
18.7 |
13.8 |
9.65 |
|
Iopt |
992 |
942 |
742 |
527 |
|
Ik |
140 |
336 |
474 |
316 |
Table 5. Values of maximum production rate, PBmax (mgC
mgChla-1 h-1) of phytoplankton populations from different locations.
|
Authors |
Locations |
PBmax |
|
Lalli & Parsons (1993)
|
Several |
0.2 - 17 |
|
Côté & Platt (1983) |
Bedford Basin, Nova Scotia |
2.04 - 8.37 |
|
Savidge (1988) |
Strangford Lough, Northern
Ireland |
0.28 - 20.48 |
|
Riegman and Colijn (1991) |
North Sea |
0.80 - 35.80 |
|
Kromkamp and Peene (1995) |
Schelde Estuary,
Netherlands |
0.50 - 18.80 |
|
Present study |
Tagus Estuary, Portugal |
9.56 - 36.30 |
Table 6. Equations of the oxygen dissolved model.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Phyto- Phytoplankton biomass (mgChl a l-1) O2 - Dissolved oxygen concentration (mgO2 l-1) P- Oxygen production (mgO2 l-1 min-1) R - Respiration (mgO2 l-1 min-1) Resp. rate. - Experimentally determined respiration rate (mgO2 mgChl a-1 min-1) PB (I,t) - Production rate (eq. 10)(mgO2 mgChl a-1 min-1) PBmax - Maximum production rate (mgO2 mgChl a-1 min-1) Iopt - Optimal light intensity (mE m-2 s-1) a - Initial slope of the P-I curve (mgO2 mgChl a-1 min-1mE-1 m2 s) t - time (minutes) |