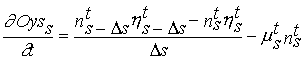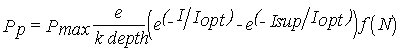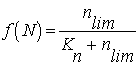Trophic
capacity of Carlingford Lough for oyster culture - analysis by ecological
modelling
Ferreira,
J.G.1, Duarte, P.2
and Ball, B. 3
1 Universidade
Nova de Lisboa, Fac. Ciências e Tecnologia, DCEA, Quinta da Torre, 2825 Monte de Caparica, Portugal;
2 Universidade
Fernando Pessoa, Dep. de Ciências e Tecnologia, Praça 9 de Abril, 349, 4200
Porto, Portugal; e-mail: nop57746@mail.telepac.pt
3
The Martin Ryan Marine Science Institute,
University College Galway, Galway, Ireland; e-mail:
brendan.ball@ucg.ie
Abstract
A one-dimensional ecosystem box model is presented for
carrying capacity assessment. The model includes physical and biological
processes. The physical processes are the transport of nutrients, suspended
matter and phytoplankton through the system boundaries and between model boxes.
The biological processes are primary production and oyster (Crassostrea
gigas) population dynamics and physiology. The model was implemented using
an object-oriented approach. The model was employed to estimate the carrying
capacity of Carlingford Lough (Ireland) for oyster culture. In the Lough, low
water temperatures prevent the oysters from reproducing. Therefore, recruitment
is human-dependent. Small oyster spat is seeded every year during spring and
harvested after the summer of the next year. During this period oysters reach
commercially harvestable weight. The results obtained indicate that the
carrying capacity of this system is approximately 0.45 g oysters (AFDW) m-3,
determined more by the availability of particulate matter than by
phytoplankton. It is suggested that a five-fold increase in oyster seeding may
optimise harvest yield.
Key words: Carrying capacity, oyster culture, demographic modelling.
Introduction
The carrying
capacity may be defined as the stock density at which production levels are
maximised without negatively affecting growth rates (Carver & Mallet,
1990). Due to the lack of proper
management strategies bivalve cultivation often exceeds the carrying capacity
of the environment, therefore reducing harvest yields and potentially
compromising sustainability. The importance of modelling for carrying capacity
assessment was discussed by Heral (1993); other authors (Bacher, 1989; Raillard
& Ménesguen, 1994) assessed carrying capacity in a macrotidal shellfish
system (Marennes-Oléron Bay in France), by means of an ecological model.
The previous authors
used a physical and a biological sub-model. The physical sub-model simulated
the transport of dissolved and particulate matter whereas the biological
sub-model simulated the assimilation of the latter by an oyster population. The
model of Bacher (1989) did not simulate primary productivity, assuming that the
renewal of food by primary production is negligible when compared to the inputs
by tidal currents at the ocean boundary. The oyster (Crassostrea gigas)
population was the only biological variable explicitly simulated. The model of Raillard & Ménesguen (1994)
simulated phytoplankton and zooplankton growth. The nitrogen cycle was also
considered due to the role played by primary production. However, the
deposition and resuspension of sediments within the model boxes were not
considered.
The overall
methodology in these models was identical. The ecosystem was assumed to be
vertically homogeneous and divided into compartments (model boxes). Although
the number and shape of the chosen compartments differed, in both cases the
models were bidimensional and the size of the compartments was comparable to
the tidal excursion (Bacher, 1989; Raillard & Ménesguen,1994).
In the present
study the system was also divided into "large" ecological boxes (see
Fig. 1) with the transport of particulate and dissolved substances between
boxes calculated using an upwind 1-D transport scheme. However, instead of
using the classical approach of dividing the model into a physical and a
biological sub-model each with their state variables, an object-oriented
approach was followed and the system divided in functional ecological units
(objects), each with their state variables and forcing functions. For details
regarding object-oriented programming (OOP) see e.g. Schildt (1995). Sekine et
al. (1991), Silvert (1993) and Ferreira (1995) discuss the utility and some
applications of OOP in ecosystem modelling. The latter paper gives a detailed
description of the programming approach used in the development of the present
model (EcoWin). Some further details are given in the methods section.
The main objectives of the present work were the
following:
·
To simulate oyster growth in
Carlingford Lough by means of an ecological model;
·
To assess the carrying capacity of
Carlingford Lough for the cultivation of the Pacific Oyster, and examine
different management strategies for aquaculture;
·
To perform a mass balance for
nitrogen in the Lough, in order to understand the relative importance of
physical and biological variables;
·
To test and discuss the usefulness
of the model against the results obtained.
The study area
Carlingford Lough
is a small embayment on the Irish east coast, forming part of the border
between the Republic of Ireland and Northern Ireland (Fig. 1). It is 16.5 km
long and 5.5 km wide at its widest point, with an area of approximately 40 km2
and an average depth of 5 m. The mean tidal prism corresponds to about 50% of
the mean Lough volume. It has important intertidal areas in the north and south
margins that correspond to almost half of the total area. The main freshwater
discharge is from the Newry (Clanrye) river, with a small flow rate that can
vary from 1 m3s-1 in Summer to 9 m3s-1
in Winter ( roughly 105-106 m3d-1).
(Fig. 1 near
here)
In
Carlingford Lough the oysters need approximately 1.5 years to reach a
commercially valuable size, which was the period required in Marennes-Oléron
when oyster culture was initiated, in clear contrast with the present 4-year
period (Raillard & Ménesguen, 1994). There are several possible reasons to
explain the differences in growth rates between both cultivation areas and
these will be discussed below. However, the most obvious seems to be the
difference in oyster density, since it was demonstrated by Bacher (1989) and
confirmed by Raillard & Ménesguen (1994) that density correlates negatively
with individual growth. In Marennes-Oléron Bay the oyster density in the boxes
used for cultivation is approximately 6 individuals m-3 (calculated
from Raillard & Ménesguen, 1994) whereas in Carlingford Lough it is over
100 times lower (approximately 0.05 individuals m-3).
In
Carlingford Lough the oyster recruitment is human-dependent. The oysters
develop gametes but spawning does not occur, presumably because the temperature
never reaches the required level. Oyster seeding takes place every year in the
months of May and June - approximately 5 tonnes of spat. After two summers the
oysters are harvested, by which time their biomass has increased to 300 - 400
tonnes. The oyster cultivation areas are located in boxes 2 and 3 (Fig. 1).
Although box 1 seems to have good conditions for oyster growth, bacterial
contamination from domestic and cattle effluents prevents its use as a
cultivation area.
Methods
The modelling
approach followed in the present study may be divided in four parts:
1) Data loading
and exploration for model calibration and validation by means of the database
BarcaWin;
2) Box definition
with DifWin;
3) Application of
the hydrodynamic model for calculation of dispersion coefficients, and in order
to refine box definition;
4) Model
development and simulations with EcoWin.
BarcaWin
is a relational database that includes a program for file conversion between
different formats, the data files, and database software for analysis and exploration
of the data. The BarcaWin database is written in Turbo Pascal for Windows and
C++, and uses the Borland Paradox Engine for all database-related functions.
DifWin allows the interactive definition of the physical compartments in a
box-model. The software is a tool allowing easy linkage between an ecological
and a hydrodynamic model. It generates two kinds of outputs: the compartment
definition and its morphological parameters (areas and volumes). For further
details see Vicente (1994). It uses as input the bathymetry files defined for
hydrodynamic modelling, which typically have a resolution one to two orders of
magnitude greater than the boxes used in ecological models. A digitised
bathymetry for the system of interest must be obtained from existing charts or
digital data. The definition of the compartments is made over the hydrodynamic
model grid and the output generated consists of the identification of which
hydrodynamic grid cells are contained in each ecological compartment. This
information is used by the hydrodynamic model to calculate the dispersion
coefficients between the ecological model boxes. The second kind of output, the
compartment's morphological parameters, is used directly by the ecological
model.
A
2-D finite difference, vertically integrated hydrodynamic model with a 71m grid
size was applied to the Lough. The definition of the ecological boxes was
refined depending on the advective patterns obtained from the hydrodynamic
model. Since the ecological model is tidally averaged, the hydrodynamic model
was used to compute the dispersion coefficients for the large boxes. A
complementary methodology was applied following the steady-state mean salinity
approach described in Barretta & Ruardij (1988), taking advantage of the 1-D formulation of the ecological model.
Both methods gave good agreement.
The
EcoWin ecological model is written in C++, and is based on the object-oriented
paradigm. The ecosystem is divided into objects that represent the different
functional compartments in the model. The objects encapsulate attributes
(variables) and methods (procedures and functions). Object properties are
inherited by descendants, making it possible to establish object hierarchies
which greatly improve code reusability and security, and the sensitivity of
different compartments in the model may easily be tested by switching their
objects on or off.
The objects defined for Carlingford Lough in the
EcoWin shell are the following:
·
Forcing functions
·
Advection-dispersion
·
Suspended particulate matter
·
Phytoplankton
·
Oysters
·
Man
Forcing function
objects
The
model is forced by river flow, temperature and light. River flow is simulated
by a flow object from an empirical relationship between time of the year and
river flow, established with field data. Photoperiod and light intensity are
calculated by a light object using standard formulations described in Brock
(1981) and Portela & Neves (1994). Temperature is calculated by a
temperature object from an empirical relationship between time of the year and
water temperature.
Advection-dispersion
object
For any physical compartment (box) in the model, the change of a
property (e.g. dissolved substances) with time may be calculated by summing the
total advective flows in/out of the box and the total dispersive flows in/out
of the box, and adding a term representing non-conservative processes (internal
sources and sinks). The sources and sinks for non-conservative substances are
calculated by other objects (see below) but the fluxes of those substances
between the different model boxes are calculated by the transport object.
Dissolved substances object
The dissolved substances object encapsulates the attributes and methods
for all dissolved nutrients in the system. Ammonia, nitrite and nitrate are
considered, as well as dissolved
inorganic nitrogen (DIN: NH4+ + NO2-
+ NO3-). The concentration of DIN (and its component
nutrient salts) is modified by nutrient removal by phytoplankton production,
and nutrient addition by excretion by bivalves and phytoplankton mortality
(Table 1) . The particulate organic detritus (non-living POM) is
"instantly" remineralized in the present model, with dissolved
nutrients being returned by the relevant objects as ammonia. The nutrient
object then carries out nitrification, which uses a fixed rate of oxidation of
reduced forms of DIN.
Suspended particulate matter object
The suspended particulate matter (SPM) object is described in more
detail due to the importance of the seston in the oyster growth in the Lough.
It has three state variables for Carlingford. It is responsible for calculating
the SPM concentration in each model box, for calculating the labile POC
fraction of the SPM, and also for calculating values for the light extinction
coefficient in each box. Suspended particulate matter is fractionated into
seven classes: There are five size classes, and also two generic classes for
extensibility, which are floatable materials and marine snow. Each class is
characterised as follows:
- Settling velocity (m day-1);
- Density (g cm-3);
- Equivalent spherical diameter (ESD, mm);
- phi (log2 particle size in mm) (Wentworth scale);
- Percentage of organic matter (%).
Deposition
of suspended matter
The deposition of suspended matter is calculated by the object's methods
using the following approach: the suspended matter in the water column is
fractionated into different size-classes, using equation 1 (Stumm & Morgan,
1981).
(Eq.
1)
where:
nd
: number of particles in a size-class per liter
a : coefficient related to the total SPM concentration in mg l-1
dp : particle diameter
(mm)
b : Empirical exponent
The settling speed for each grain class is calculated according to
Stokes' law. The density of the water-column is based on the current salinity
and temperature values in each box. Particle settling is related to grain-size,
and the size distribution is related (among other factors) to flocculation
processes (implicitly considered in Equation 1).
The sedimentation rate is calculated using the ratio between the
settling speed (m day-1) and the box depth, resulting in a decrease
in SPM flux. As with all other variables, this is integrated at the end of each
time-step to provide the new value for the state-variable (Table 1).
Parameterization
of deposition coefficients
The coefficients used in equation 1 were parameterized by taking the
value for b as 4 (Stumm & Morgan, 1981), considering that an equal
volume of particles was distributed in each logarithmic size interval. a was empirically adjusted so that the sum of the
particle mass per unit volume in each size-fraction was equal to pre-defined
concentrations in the range 1 - 300 mg l-1.
Effect
of turbulence
The effect of turbulence in preventing the settling of suspended matter
is simulated by the introduction of an empirical coefficient, which effectively
reduces the downward flux of suspended matter. The coefficient used is 0.8,
which effectively means that deposition may only occur during a small part of
the tidal cycle, i.e. on or about high and low water slack. This has been
validated by tests with a hydrodynamic model.
Resuspension
Resuspension depends on the shear-stress at the sediment-water
interface, and on the nature and compaction of the sediment. Based on the
studies carried out on the benthos, and on results from the existing database
on the nature of the sediment in the different model boxes, a different
sediment resuspension rate was used for each box in the model.
Extinction
coefficient
The light extinction coefficient k is estimated empirically,
using an empirical relationship between SPM concentration in the water column
and k values, obtained from measured data. The equation used for this is
the following:
(Eq.
2)
where:
k : Light extinction coefficient (m-1);
SPM : suspended particulate matter (mg l-1).
Particulate
organic carbon
The proportion of SPM which is made up of particulate organic carbon is
estimated to vary between 0.03 and 0.05
from field data gathered in Carlingford Lough .
Phytoplankton object
Primary production is estimated from light intensity, delivered by the
respective forcing function object, and nutrient data, delivered by the
dissolved substances object. If this object is not activated by the user then
primary production is calculated solely as a function of light. The light
function is taken from Steele (1962), integrated over depth, and the nutrient
limitation is calculated by a Michaelis-Menten function (Table 2). Only
nitrogen limitation is used, because an analysis of the Redfield ratio for
dissolved nutrients indicates that nitrogen is the limiting factor.
The object also calculates exudation and respiration. In the literature,
estimates of dissolved organic carbon (DOC) losses are highly variable. Values ranging from almost zero to 90 % of
carbon fixed are given by different authors (see Jørgensen et al.,
1991). There is also variability in the literature concerning the factors
affecting DOC loss. Some authors refer increased losses with poor growth
conditions (e.g. Ittekot et al., 1981), and others have found greater
DOC exudation at high productivity rates. In this model exudation is computed
as a fixed fraction of gross production (0.1). Phytoplankton respiration is
calibrated to remove a constant proportion of the fixed carbon, thus converting
the phytoplankton gross primary production (GPP) into net primary production
(NPP). This has been defined as 0.3, based on a range of values for algal
respiration and primary production given by Jørgensen et al. (1991).
Crassostrea
gigas object
Due to the economic
importance of this species, there are already some models developed to simulate
its growth (Bacher, 1989; Bacher et al., 1991; Raillard, 1991; Raillard
& Ménesguen, 1994). In the present work the simulation of oyster growth is
carried out at two levels - the physiological level and the population level
using a physiological and a demographic model. The demographic model is based
on a series of weight classes. Oyster recruitment and harvest are
man-controlled. At the physiological level the
model equations and parameters are those used earlier by Raillard (1991)
and Raillard & Ménesguen (1994).
Excretion rates are those reported in Bernard (1974). Scope for growth is
calculated by subtracting respiration and excretion from assimilation, as
described by the previous authors. The demographic model is based on a
conservation equation for the number of individuals:
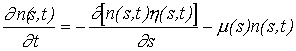(Eq. 3)
Where,
n - Number of individuals of weight s.
h - Scope for growth (g day-1).
m - Mortality (day-1).
Equations of this type have been used in demographic models for many
years (see Sinko & Streifer, 1967; Sinko & Streifer, 1969, Streifer,
1974). Equation (3) was discretized following a upwind integration scheme that
seems to be the most appropriate in transport problems (in the present case it
is transport of individuals between weight classes) (Press et al., 1995):
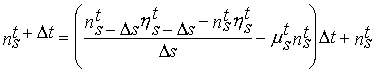(Eq. 4)
Ds - Class amplitude.
In this equation the population is discretized in size/weight classes
and s refers to the weight of each class. The scope for growth
calculated at the physiological level is then used in (4) to calculate transitions of individuals
between weight classes. A total of forty size classes between 0.65 g (FW) and
97.75 g (FW) were used. The class amplitude was 2.5 g (FW). The choice of
classes was made after running the model with various numbers of classes until
the model solution became stable taking always into consideration the Courant
condition. The first class corresponds to the juvenile oysters seeded in the
Lough.
At every time step the biomass of the different classes is calculated as
the product of the number of individuals they contain and the class weight.
Seeding, natural mortality and harvesting mortality are calculated and
added/subtracted to the numbers and biomass of each class. Natural mortality
was determined experimentally in Carlingford Lough for oysters of various sizes
(Douglas, 1992).
(Table 1 near
here)
(Table 2 near
here)
Man object
This object allows the simulation of different management strategies.
Seeding and harvesting are carried out according to normal rates (Standard
simulation) or to different rates to estimate the carrying capacity of the Lough.
Normal seeding rates correspond to an average of 0.08 tons of oysters per day
during May and June. Harvest is carried out during autumn and in the model a
constant rate of 4.6 tons per day is
used. Whenever necessary a higher rate is assumed in order to remove all the
commercial sized oysters before the end of the year. The model calibration and
validation has been described elsewhere (Ball et al., 1994), showing results
for measured data and simulations of pelagic
state variables and oysters. The model runs were performed for a simulation
period of four years, using a time step of two hours. EcoWin has variables to
save the inputs and outputs to the objects calculated at every time step. It
also allows the storage of boundary fluxes due to advection and dispersion of
pelagic state variables. It is thus possible to use the model to compute
integrated production, average standing stocks and mass budgets for all state
variables.
Results and discussion
Six
model simulations were carried out in order to assess the carrying capacity of
Carlingford Lough for oyster culture and its sensitivity to different nutrient
loads. The standard simulation
represents the present situation in the Lough, both regarding nutrient loads
and oyster standing stocks. The next three simulations were carried out to test
the effects of seeding increase of small oyster spat by 5, 10 and 20 times the
actual rate. In the last two simulations the nitrogen loads were changed by -50
% and +100 %, keeping everything else as in the standard simulation. In all
simulations the man object interacts with the oyster object through seeding and
harvest of large (> 65 g FW) oysters. Seeding is simulated during May and
harvest between the beginning of fall and the end of the year.
In
Figs. 3 and 4 predicted and simulated chlorophyll and suspended matter
concentrations are shown. Because the observed data has a significant scatter,
it is very difficult to judge the quality of the model results. However, the
simulated values are well within the range of observed data. There is a
chlorophyll peak at the end of spring or beginning of summer. This peak results
from a combination of high light intensities with nitrogen concentrations
ranging from 10 to 20 m
mol N l-1 (Ball et al., 1994). Observed data on suspended
matter do not follow any particular pattern. The model results show average
values that are close to those observed in the Lough (between 20 and 30 mg l-1).
Mass
balances
The
execution of a mass balance is very useful both for model analysis and in
analysing the ecosystem being modelled:
·
The role of physical
(advection-dispersion) and biological processes within each box may be
determined, i.e. the role of internal processes may be compared with the
throughput of material;
·
It allows an assessment of the
relative importance of the different biological state variables within each
box;
·
Residence times may be calculated
for different model variables, allowing an analysis of turnover of water
relative to other variables such as DIN or phytoplankton;
·
Inaccuracies in the mass balance
closure are an effective indicator of problems with the model, leading to
improvements in the formulation. These are not always obvious in graphical
output of results, where errors may cancel each other out.
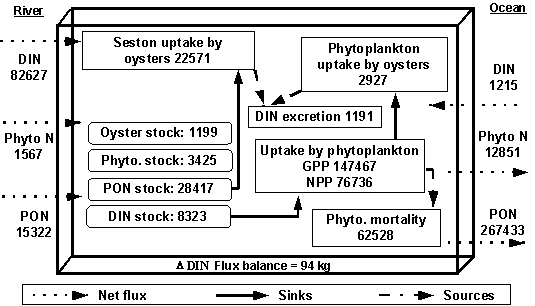
The mass balance
for dissolved inorganic nitrogen (DIN), phytoplankton and particulate organic
nitrogen (PON) is presented in Tables 3, 4 and 5. The results were obtained for
the standard simulation, and are normalised per unit of surface area to allow a
comparison with other systems.
(Table
3 near here)
The mass balances
are presented separately for physical inputs and outputs and biological sources
and sinks. The Lough imports dissolved nitrogen both from riverine sources and
from the Irish Sea (Table 3). The DIN is converted to particulate N by the
phytoplankton, some of which is exported to the Irish Sea (0.29 g N m-2
yr-1) (Table 4). Internal
sources of DIN in the model are natural phytoplankton mortality and DIN excretion
by the oysters. The natural mortality and filtration by oysters of the
phytoplankton are living particulate N sinks in the model (Table 4).
(Table 4 near here)
The PON mass
balance (Table 5) shows that PON is exported from the Lough to the Irish Sea,
and that the oyster filtration of seston is approximately one order of
magnitude greater than that of phytoplankton. Although the sediment
resuspension exceeds deposition, it corresponds only to a negligible net
resuspension of a layer 4 X 10-7 mm thick (sediment density of 2600
kg m-3).
(Table
5 near here)
(Fig.
2 near here)
From Fig. 2 it
can be seen that the upstream nitrogen input is largely in the form of DIN, and
that the largest internal sink of DIN is phytoplankton production.
Phytoplankton biomass turnover is equal to 22.4 yr-1, which is in
the range indicated by other authors (e.g. Valiela, 1995). The oysters excrete
about 5% of their nitrogen uptake, and the nitrogen removal due to them is
relatively small compared to the upstream inputs. The relation of biological
inputs to physical inputs shows that for DIN mass flux, physical processes are
more important, whereas for phytoplankton, biological processes dominate. As
regards outputs, biological processes are far more important than physical
ones, both for DIN and phytoplankton. This contrasts with other ecosystems
(e.g. Grillot & Ferreira, 1996), where the exchange of material across the
system boundaries plays a greater role than internal recycling. Tables 3, 4 and
5 and Fig. 2 show that the influence of
the oysters in the processes of phytoplankton and particulate matter sinking
and as a dissolved nitrogen source is negligible.
Oyster
growth and production
In
Fig. 5 oyster growth predicted by the model and measured in field experiments are
shown. The experimental data are described in Douglas (1992). The model results
tend to overestimate oyster growth in box 2. Since the same set of parameters
is used to simulate the oyster growth both in box 2 and 3, any parameter tuning
to improve box 2 results would tend to underestimate oyster growth and
production in box 3 beyond reasonable levels. Additionally, it was not possible
to decrease oyster growth in box 2 and box 3, and at the same time maintain the
total biomass production within the normal levels (c.a. 400 tonnes year-1).
The
oysters in Carlingford Lough do not exhibit any diminishing trends in their
individual weight over the annual cycle (Fig. 5). This is because they do not
reproduce and therefore do not lose weight through gamete emission as in
Marennes-Oléron Bay (Bacher, 1989). The losses through respiration, the smaller
amount of organic seston and the lower temperatures prevent any significant
growth during winter. Growth in box 2 is higher than in box 3 due to higher
phytoplankton concentrations in the former (Fig. 3).
(Fig. 5 near here)
In
Figs 6 and 7 the biomass dynamics of the forty oyster weight classes is shown
for a period of two years. Three cohorts can be observed in Fig. 6 and four in
Fig. 7. The beginning of a cohort is located between days 120 and 180 (May and
June) when seeding takes place. The growth of the cohort may be followed to the
right of Figs 6 and 7. The growth acceleration is clearly seen during spring
and summer. After day 265 there is a sudden decrease in the biomass of the
large oysters due to harvest. All oysters above 65 g (FW) are harvested. By
following the cohort from seeding to harvest it is possible to estimate the
number of months it takes for the oysters to reach a commercial size - between
about 12 months in box 2 and 17 months in box 3. The sharp peaks observed in
Fig. 6 indicate a greater biomass concentration in the largest oysters in
excess of that observed in box 3. The model predicts a 325 tonnes (FW) harvest
in box 2 and 42 tonnes (FW) in box 3 after two summers. Both results are well
within the real values (Douglas, pers. comm.).
(Figs
6 and 7 near here)
The
next figures synthesise results obtained with model simulations of different
seeding rates. In Fig. 8 and 9 the average individual weight of the oysters is
plotted against time for different average standing stocks in box 2 and 3.
These standing stocks resulted from different seeding rates as explained
earlier. All lines follow a similar pattern with a decreasing trend after seeding,
when a large number of small spat is introduced in the Lough and after harvest,
when the largest oysters are removed from the system. It is clearly seen that
the larger the standing stock the smaller tends to be the average individual
weight. This negative relationship suggests intraspecific competition for food
at higher than normal standing stocks.
(Figs
8 and 9 near here)
The
maximum value for oyster productivity was obtained for the standard simulation
corresponding to 1370 mg g-1 year-1 (Fig. 10). These
values were averaged for both boxes. It is clearly seen that oyster
productivity declines sharply as standing stock increases. The time taken to
reach a harvestable size increases very fast with seeding (Fig. 11). When
seeding is increased to 10 times its normal value, the time to reach an
harvestable size is more than two years. In this hypothetical scenario the
oysters seeded during the spring of one year would not grow fast enough to be
harvested after the summer of the next year as is presently the case in
Carlingford Lough. It is important to note that the present model simulates
cohorts based on weight rather than on age. The time needed to reach an
harvestable size was determined graphically following the cohorts since their
seeding. It is theoretically possible that animals of different ages appear in
the same weight class. This may happen with two cohorts born in different years
when the first one had to survive through a period of poor growth conditions.
In the present case this did not happen because the model forcing did not
differ from one year to the next. An important improvement in the demographic
model would be the implementation of a age-weight equation as described in Sinko & Streifer (1967). This would
give the model more flexibility and utility in management terms.
Harvest
can be maximised by increasing the actual seeding rates approximately 5 times
(Fig. 12). Above these values the increase in harvest is very small and
according to the previous results the oysters will take much more time to reach
a harvestable size. These results suggest a maximum sustainable yield around
1300 tons of commercial sized oysters per year. The simulations with seeding
increased 10 and 20 times produced a average oyster density of about 0.92 and 1.6 individuals m-3.
These values are still well below the 6 individuals m-3 of
Marennes-Oléron Bay (Raillard & Ménesguen, 1994) but growth depression is
apparent. The differences between both systems may be at least in part due to
the higher productivity in Marennes-oléron bay (see paper in this volume).
(Figs
10, 11 and 12 near here)
In
all model simulations oyster mortality was calculated solely as a function of
individual weight using the experimental results described in Douglas (1992).
According to Raillard & Ménesguen (1994) oyster mortality tends to increase
with oyster density. If this dependence was included in the model the
differences between the simulations would be even more pronounced.
The
sensitivity of the model to changing nitrogen loads was not very noticeable in
terms of oyster production . The model predicted that a decrease of 50 % in the
nitrogen load leads to an oyster productivity of 1340 mg g-1 yr-1
whereas a 100 % increase leads to a productivity of 1390 mg g-1
yr-1 . These values are very close to those obtained under the
standard simulation (1370 mg g-1 yr-1). This may be
explained because oyster growth in Carlingford Lough depends more on
particulate matter, rather than on phytoplankton biomass.
A
possible weakness of the model is in the way scope for growth is calculated,
because the equations use constant parameters over the all simulation period.
However, as discussed by Bayne (1993) these parameters change as a result of physiological
and morphological adaptation of the filter-feeders at various time-scales. An
important step in model refinement would be the description of oyster
feeding based on principles of
optimality (Willows, 1992). It is important to note that the usage of average
exchange coefficients between model compartments implies that part of the
system dynamics, namely that resulting from the tide excursion, is lost.
Considering the non-linearities between the biological processes and the
environmental conditions it is likely that these averaging procedures may lead
to some distortion of the results.
Conclusions
Carrying
capacity models are necessary to predict responses of bivalve growth rate in
relation to different management strategies (Heral, 1993). Carlingford Lough is
an example of a system where bivalve cultivation is still below the level where
oyster growth begins to be inhibited by stock density. Furthermore, since the
oysters are not able to reproduce within the Lough due to low water
temperatures, it is easier to control the population. According to the model
results it seems likely that a five-fold increase in seeding would maximise
oyster production in the Lough, allowing harvest to grow from the present
300-400 tonnes to a level of 1300
tonnes year-1 without significantly affecting the oyster growth
rate. Further increases in seeding do not seem to lead to very significant
increases in large oysters. Therefore, according to the definition of carrying
capacity quoted previously, it may be stated that the carrying capacity of
Carlingford Lough is approximately 0.44 g (AFDW) m-3 (see Fig. 10) or 0.26 oysters m-3.
In
its present form, the model allows a fast and easy simulation of different
seeding and harvesting strategies, with direct access to all model parameters
and results. The model predictions generally show a reasonable agreement with
observed data, making it a useful tool for carrying capacity assessment.
However, the small number of model boxes may cause some bias on the results.
The main oyster cultivation areas in box 3 are located very close to the
boundary between box 2 and 3. For this reason it is likely that in this area
the environmental conditions may be closer to those of box 2 than predicted by
the model. This could help to reduce the differences in predicted oyster growth
in boxes 2 and 3 (Fig. 5).
The
usage of a demographic model proved to be useful in obtaining a detailed
description of the biomass dynamics of the studied species. When the objective
is to optimise a sustainable yield, it is important to know the harvestable and
non-harvestable classes and the rate at which the population recovers from the
harvest (Usher, 1966). Although the usage of the demographic model
significantly increases the computing time, the coupling between the
physiological and the demographic processes seem to be the best solution to
simulate biomass dynamics of a exploitable resource. This coupling allowed the
advantages of the general dynamic population models and analytical models (sensu
Heral, 1993) to be synthesised in one model.
The
combination of the three key components of, a large-scale coupled
physical-ecological model, detailed physiological modelling of the target
species, and the demographic aspects which are fundamental to aid decision-making
for management purposes, appears to be generally applicable to carrying
capacity assessment for bivalve species. This modelling approach further
benefits from the object-oriented methodology used - it allows for easy
development of the code to incorporate more species, and the pre-processing
tools employed make it straightforward to apply the same model to different
estuarine and coastal ecosystems.
Acknowledgements
This work was
supported by EU FAR project AQ-2-516 "Development of an Ecological Model
for Mollusc Rearing Areas in Ireland and Greece” and by EU Concerted Action
AIR3-CT94-2219 "Trophic capacity of coastal zones for rearing oysters,
mussels and cockles". The authors wish to thank two anonymous referees for
helpful suggestions.
References
Bacher C (1989) Capacité trophique du bassin de Marennes-Oléron:
couplage d'un modèle de transport particulaire et d'un modéle de croissance de
l'huître Crassostrea gigas. Aquat. Living Resour. 2: 199 - 214
Bacher C, Héral
M, Deslous-Paoli and Razet D (1991) Modèle énergétique uniboite de la
croissance des huîtres (Crassostrea gigas) dans le bassin de
Marennes-Oléron. Can. J. Fish. aquat. Sci. 48: 391 -
404
Ball
B, Ferreira JG and Keegan B (1994) Development of a model to determine the
trophic capacity of mollusc rearing areas in Ireland and Greece. Final Report
to the CEC for project FAR-AQ2516
Baretta J and Ruardij P (eds) (1988) Tidal flat estuaries. Simulation
and analysis of the Ems Estuary. Springer-Verlag, Berlin
Bayne BL (1993) Feeding physiology of bivalves: Time dependence and
compensation for changes in food availability. In: R.F. Dame (ed.). Bivalve
filter feeders in estuarine and coastal ecossystem processes. (pp. 1 - 24)
Springer-Verlag, Berlin
Bernard FR (1974) Annual biodeposition and gross energy budget of mature
pacific oysters, Crassostrea gigas. J. Fish Res. Bd Can. 31: 185-190
Brock TD (1981) Calculating solar radiation for ecological studies.
Ecol. Modelling 14: 1 - 9
Carver CEA and Mallet AL (1990) Estimating carrying capacity of a
coastal inlet for mussel culture. Aquaculture 88: 39 - 53
Douglas DJ (1992) Environment and Mariculture (A study of Carlingford
Lough). Ryland Research Ltd., Ireland
Ferreira JG (1995) EcoWin - An Object-oriented Ecological Model for
Aquatic Ecosystems. Ecol. Modelling 79: 21 - 34
Grillot N and Ferreira JG (1996). Ecological model of the Cala do
Norte of the Tagus Estuary. ECOTEJO, Rel. A-8403-06-96-UNL, Ed. DCEA/FCT, New University of Lisbon
Heral M (1993) Why carrying capacity models are useful tools for
management of bivalve molluscs culture. In: R.F. Dame (ed.). Bivalve filter
feeders in estuarine and coastal ecossystem processes. (pp. 455 - 477)
Springer-Verlag, Berlin
Ittekot V, Brockmann U, Michaelis W and Degens ET (1981) Dissolved, free
and combined carbon hydrates during a phytoplankton bloom in the Northern North
Sea. Mar. Ecol.
Progr. Ser. 4: 259-305
Jørgensen SE, Nielsen S and Jørgensen L (1991) Handbook of Ecological
Parameters and Ecotoxicology. Elsevier, Amsterdam
Portela LI and Neves R (1994) Modelling temperature distribution in the
shallow Tejo estuary. In: Tsakiris & Santos (ed). Advances in Water
Resources Technology and Management. (pp. 457 - 463) Balkema, Rotterdam
Press WH, Teukolsky SA, Vetterling WT
and Flannery BP (1995) Numerical recipes in C - The art of scientific
computing. Cambridge University Press, Cambridge
Raillard O (1991) Etude des interactions entre les processus physiques
et biologiques intervenant dans la production de l'huître japonaise Crassostrea
gigas du bassin de Marennes-Oléron: essais de modélisation. Thèse doct.
Océanographie, Univ. Paris VI
Raillard O and Ménesguen A (1994) An ecosystem box model for estimating
the carrying capacity of a macrotidal shellfish system. Mar. Ecol. Prog. Ser.
115: 117 - 130
Schildt H (1995) C++, the complete reference, 2nd. Edition. Osborne
Sekine M, Nakanishi H, Ukita M and Murakami S (1991) A shallow-sea
ecological model using an object-oriented programming language. Ecol. Modelling
57: 221-236
Silvert W (1993) Object-oriented ecosystem modelling. Ecol. Modelling
68: 91-118
Sinko JW and Streifer W (1967) A new model for age-size structure of a
population. Ecology 48: 910 - 918
Sinko JW and Streifer W (1969). Applying models incorporating age-size
structure of a population to Daphnia. Ecology 50: 608 - 615
Steele JH (1962) Environmental control of photosynthesis in the sea.
Limnol. Oceanogr. 7: 137 - 150
Streifer W (1974) Realistic models in population biology. Adv. ecol. Res.
8: 199 - 266
Stumm W and Morgan J., (1981) Aquatic Chemistry, 2nd. Edition.
Wiley-Interscience
Usher MB (1966) A matrix approach to the management of renewable
resources, with special reference to selection forests. J. appl. Ecol. 3: 355 -
367
Valiela I (1995) Marine ecological processes, 2nd Edition.
Springer-Verlag
Vicente P (1994) DifWin: A package for the definition of compartments
and calculation of dispersion coefficients in box models - Application to the
Carlingford Lough. In: Proceedings of the First International Conference on
Hydroinformatics, Delft, Netherlands, 717- 721
Willows RI (1992). Optimal digestive investment: A model for
filter-feeders experiencing variable diets. Limnol. Oceanogr. 37: 829 - 847
Table
1. Main model equations and corresponding processes. These equations consider
the sources and sinks for each model box. The transport equation calculates
mass transfer between model boxes. Parameter values were taken from the
literature (e.g. Jørgensen et al., 1991) and tuned to calibrate the
model.
|
Suspended
particulate matter (mg
l-1)
|
(5) |
||||
|
ds |
Suspended matter deposition rate |
Calculated from particle-size distributions and Stokes’ law (see text) |
|||
|
Dissolved
mineral nitrogen (mmol l-1)
|
(6) |
||||
|
ppN |
Phytoplankton gross photosynthetic rate calculated by eq. 14 and
converted to nitrogen units. |
|
|||
|
Phytoplankton (mg Chla l-1)
|
(7) |
||||
|
pp |
Phytoplankton gross photosynthetic rate |
h-1 (eq. 14) |
|||
|
ep |
Phytoplankton exudation rate |
0.3 of pp |
|||
|
rp |
Phytoplankton respiration rate |
0.3 of pp |
|||
|
mp |
Phytoplankton mortality |
0.002 h-1 |
|||
|
gOys |
Oyster grazing pressure |
h-1 |
|||
|
CarbonToChlrophyll |
Conversion factor |
0.03 |
|||
|
Oysters |
|
||||
|
Oyster number for each class
|
(8) (see text) |
||||
|
h |
Individual oyster scope for growth |
As
in Raillard (1991) and Raillard & Ménesguen (1994) |
|||
|
ms |
Oyster mortality of the sth class |
(See text) |
|||
|
Fresh weight to ash free dry weight |
|
0.05 |
|||
|
In the first class recruitment must also be added to eq. 8 |
|||||
|
For classes where oyster weight is above 65 g (FW) harvest may also
occur, in which case it must be subtracted from eq. 8. |
|||||
Table
2. Rate equations for the biological processes and parameter values. Parameter
values taken from the literature (e.g. Jørgensen et al., 1991) and tuned
to calibrate the model.
|
Phytoplankton |
|
|
|
|
(9) |
|
|
|
(10) |
|
|
Pmax |
Maximum
photosynthesis |
0.02
h-1 |
|
I |
Light
intensity at box depth |
Calculated - m E m-2
s-1 |
|
Isup |
Surface
light intensity |
Calculated - m E m-2
s-1 |
|
Iopt |
Optimum
light intensity |
400 m E m-2
s-1 |
|
f(N) |
Nutrient
limitation |
Calculated |
|
nlim |
Nutrient
concentration |
mmol N l-1 (Delivered by the dissolved
substances object) |
|
Kn |
Half-saturation constant for limiting nutrient |
1.19 mmol N l-1 |
|
Oysters |
All equations and parameters as in Raillard (1991) and Ralillard &
Ménesguen (1994) |
|
Table 3 -
Standard simulation. Mass balance for DIN in Carlingford Lough (all fluxes in g
N m-2 yr-1).
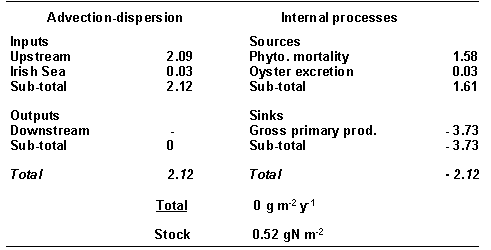
Table 4 -
Standard simulation. Mass balance for phytoplankton in Carlingford Lough (all
fluxes in gN m-2 yr-1).
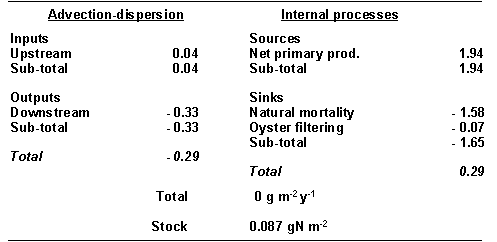
Table 5 -
Standard simulation. Mass balance for PON in Carlingford Lough (all fluxes in
gN m-2 yr-1).
|
|
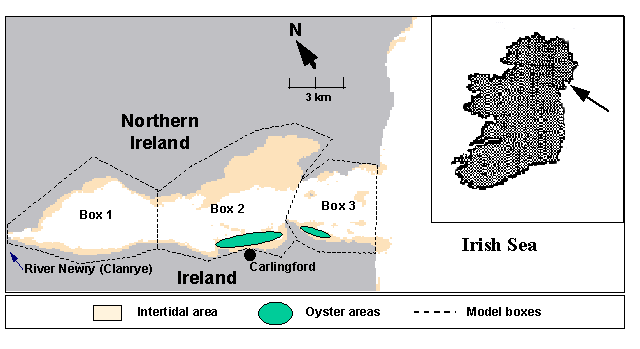
Fig. 1
|
|
Fig. 2
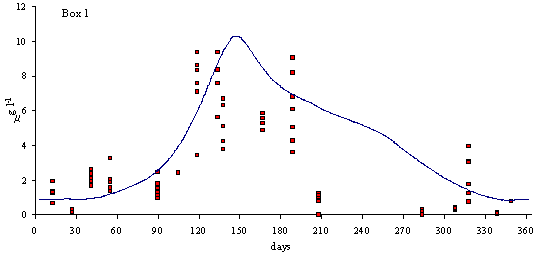
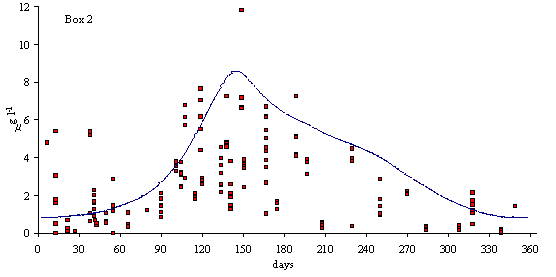
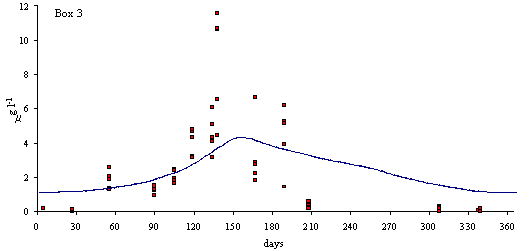
Fig. 3
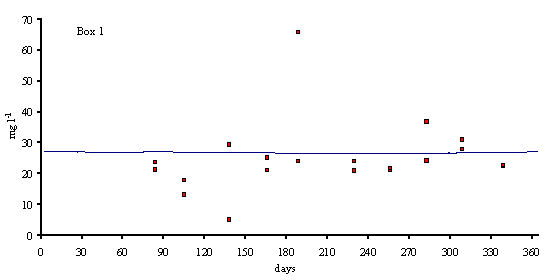
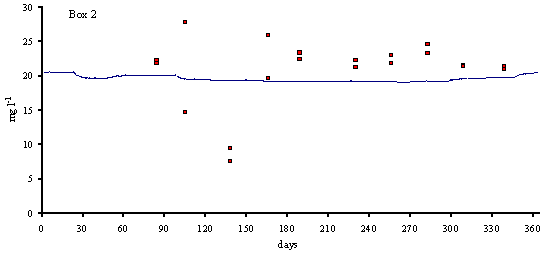
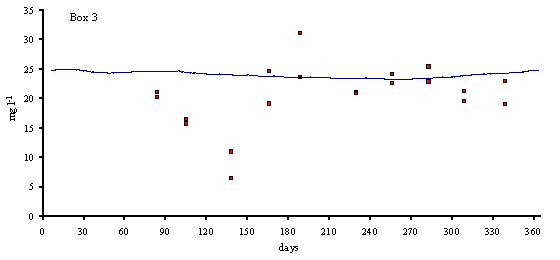
Fig. 4
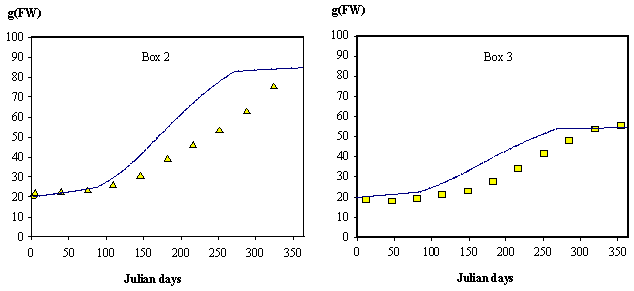
Fig. 5
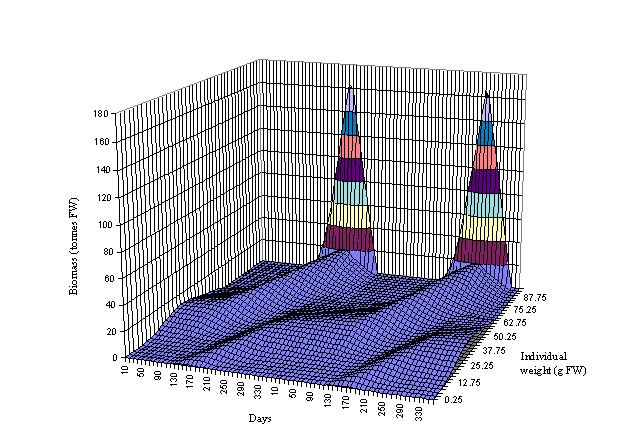
Fig. 6
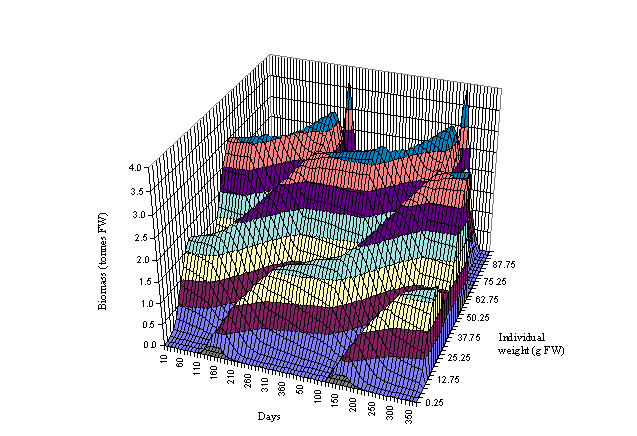
Fig. 7
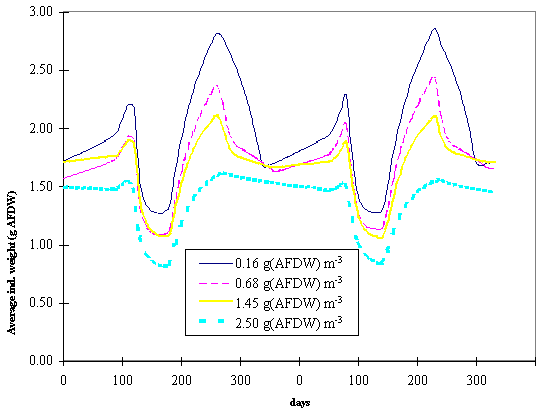
Fig. 8
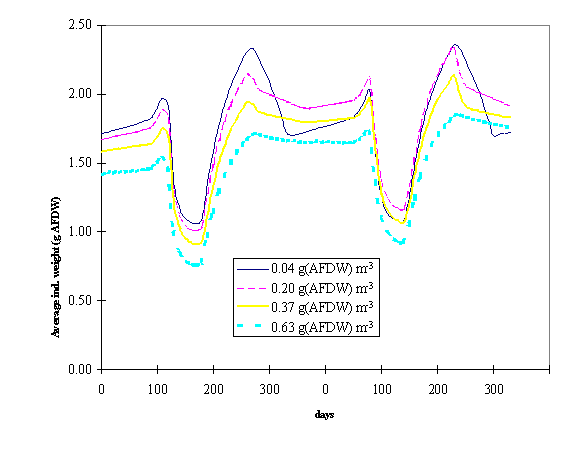
Fig. 9
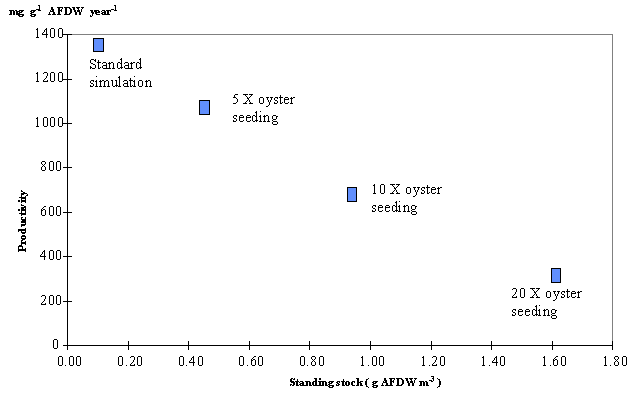
Fig. 10
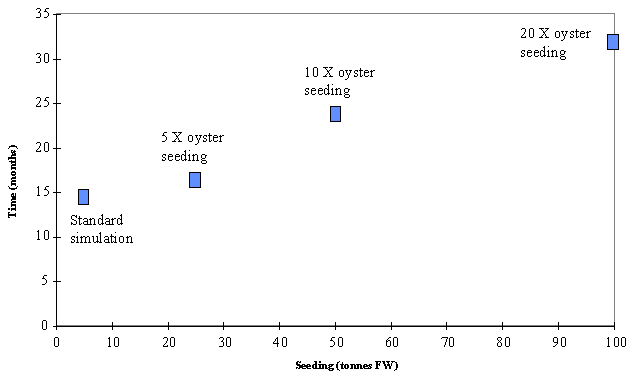
Fig. 11
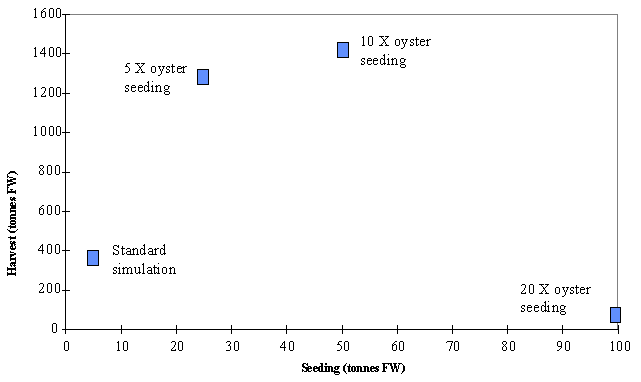
Fig. 12
Figure captions
Fig. 1 - Carlingford Lough, showing the oyster
cultivation areas and model boxes.
Fig. 2 - Standard simulation. General scheme of stocks
(rounded rectangles), fluxes (rectangles), sources and sinks of nitrogen in the
model (all values in kgN yr-1).
Fig. 3 - Standard simulation. Predicted and simulated
phytoplankton biomass in model boxes 1, 2 and 3 (mg Chlorophyll l-1).
Fig. 4 - Standard simulation. Predicted and simulated
suspended matter (mg l-1) in model boxes 1, 2 and 3.
Fig. 5 - Standard
simulation. Growth simulation of an oyster with 20 g (FW) at the beginning of
the year. Triangles and squares refer
to measurements obtained in Box 2 and 3, respectively (Douglas, 1992).
Fig. 6 - Standard
simulation. Oyster biomass in box 2 as a function of time and individual
weight. The drop in the biomass of large oysters at the end of each year
corresponds to harvest.
Fig. 7 - Standard
simulation. Oyster biomass in box 3 as a function of time and individual
weight. The drop in the biomass of large oysters at the end of each year
corresponds to harvest.
Fig. 8 - Average
individual weight of the oyster population as a function of time and under
different average standing stocks in box 2 (see text for explanation).
Fig. 9 - Average
individual weight of the oyster population as a function of time and under
different average standing stocks in box 3 (see text for explanation).
Fig. 10 - Oyster
productivity as a function of average standing stock.
Fig. 11 - Time to
reach a harvestable size as a function of seeding.
Fig. 12 - Oyster
harvest as a function of seeding after the time necessary for the oysters to
reach an harvestable size (see text).